题目内容
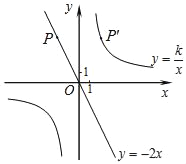
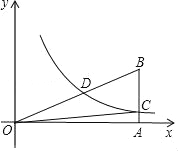
【题目】若关于x的一元二次方程x2+(2k﹣1)x+k2=0的两根a、b满足a2﹣b2=0,双曲线![]() (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
A. 3 B. ![]() C. 6 D. 3或
C. 6 D. 3或![]()
【答案】B
【解析】
首先由一元二次方程根的判别式得出k的取值范围,然后由a2﹣b2=0得出a+b=0或a-b=0,再运用一元二次方程根与系数的关系求出k的值,由k的几何意义,可知S△OBA=![]()
![]() .如果过D作DE⊥OA于E,则S△OCA=
.如果过D作DE⊥OA于E,则S△OCA=![]()
![]() .易证△ODE∽△OBA,根据相似三角形的面积比等于相似比的平方,得出S△OBA,最后由S△OBC=S△OBA-S△OCA,得出结果.
.易证△ODE∽△OBA,根据相似三角形的面积比等于相似比的平方,得出S△OBA,最后由S△OBC=S△OBA-S△OCA,得出结果.
∵x2+(2k-1)x+k2=0有两根,
∴△=(2k-1)2-4k2≥0,
即k≤![]() .
.
由a2﹣b2=0得:(a-b)(a+b)=0.
当a+b=0时,-(2k-1)=0,解得k=![]() ,不合题意,舍去;
,不合题意,舍去;
当a-b=0时,a=b,△=(2k-1)2-4k2=0,
解得:k=![]() 符合题意.
符合题意.
∵![]() ,
,
∴双曲线的解析式为:![]() .
.
过D作DE⊥OA于E,则S△ODE=S△OCA=![]() ×1=
×1=![]() .
.
∵DE⊥OA,BA⊥OA,
∴DE∥AB,∴△ODE∽△OBA,
∴![]() ,∴S△OBA=4×
,∴S△OBA=4×![]() =2,
=2,
∴S△OBC=S△OBA-S△OCA=2-![]() =
=![]() .
.
故选B.

【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.