题目内容
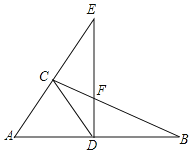
【题目】如图，点P是平行四边形ABCD边上的点，AP=
AB，射线CP交DA的延长线于点E，则S△APE：S平行四边形ABCD等于（ ）
A. 1：5B. 1：8C. 1：12D. 1：13
【答案】C
【解析】
设△AEP的面积为m．利用相似三角形的性质分别求出四边形PADC和△PBC的面积即可解决问题．
解：设△AEP的面积为m．
∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AD∥BC，
∴△EAP∽△EDC，
∴
=（
）2，
∵PA=
AB，
∴CD=3PA，PB=2PA，
∴△EDC的面积为9m，四边形PADC的面积为8m，
∵EA∥BC，
∴△EAP∽△CBP，
∴
=（
）2=
，
∴△PBC的面积为4m，
∴S△APE：S平行四边形ABCD=m：（4m+8m）=1：12，
故选：C．
练习册系列答案
相关题目
