Question

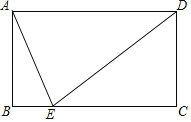
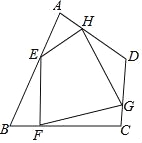
【题目】如图，ABCD、CEFG是正方形，E在CD上，直线BE、DG交于H，且HEHB=4-2，BD、AF交于M，当E在线段CD（不与C、D重合）上运动时，下列四个结论：①BE⊥GD；②AF、GD所夹的锐角为45°；③GD=AM；④若BE平分∠DBC，则正方形ABCD的面积为4，其中结论正确的是______（填序号）

Answer 1

【答案】①②③④

【解析】

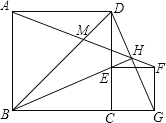
①由已知条件可证得△BEC≌△DGC，∠EBC=∠CDG，因为∠BDC+∠DBH+∠EBC=90°，所以∠BDC+∠DBH+∠CDG=90°，即BE⊥GD，故①正确；②若以BD为直径作圆，那么此圆必经过A、B、C、H、D五点，根据圆周角定理即可得到∠AHD=45°，所以②的结论也是正确的．③此题要通过相似三角形来解；由②的五点共圆，可得∠BAH=∠BDH，而∠ABD=∠DBG=45°，由此可判定△ABM∽△DBG，根据相似三角形的比例线段即可得到AM、DG的比例关系；④若BE平分∠DBC，那么H是DG的中点；易证得△ABH∽△BCE，得BDBC=BEBH，即BC2=BEBH，因此只需求出BEBH的值即可得到正方形的面积，可先求出BE、EH的比例关系，代入已知的乘积式中，即可求得BEBH的值，由此得解．

解：①正确，证明如下：

∵BC=DC，CE=CG，∠BCE=∠DCG=90°，

∴△BEC≌△DGC，∴∠EBC=∠CDG，

∵∠BDC+∠DBH+∠EBC=90°，

∴∠BDC+∠DBH+∠CDG=90°，即BE⊥GD，故①正确；

②由于∠BAD、∠BCD、∠BHD都是直角，因此A、B、C、D、H五点都在以BD为直径的圆上；

由圆周角定理知：∠DHA=∠ABD=45°，故②正确；

③由②知：A、B、C、D、H五点共圆，则∠BAH=∠BDH；

又∵∠ABD=∠DBG=45°，

∴△ABM∽△DBG，得AM：DG=AB：BD=1：，即DG=AM；

故③正确；

④过H作HN⊥CD于N，连接EG；

若BH平分∠DBG，且BH⊥DG，已知：BH垂直平分DG；

得DE=EG，H是DG中点，HN为△DCG的中位线；

设CG=x，则：HN=x，EG=DE=x，DC=BC=（+1）x；

∵HN⊥CD，BC⊥CD，

∴HN∥BC，

∴∠NHB=∠EBC，∠ENH=∠ECB，

∴△BEC∽△HEN，则BE：EH=BC：HN=2+2，即EH=；

∴HEBH=BH=4-2，即BEBH=4；

∵∠DBH=∠CBE，且∠BHD=∠BCE=90°，

∴△span>DBH∽△EBC，得：DBBC=BEBH=4，

即BC2=4，得：BC2=4，即正方形ABCD的面积为4；

故④正确；

故答案为：①②③④．