题目内容
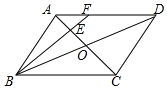
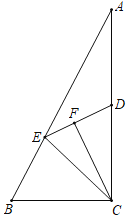
【题目】如图,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_____.
的长为_____.
【答案】2或![]()
【解析】
![]() 与
与![]() 关于
关于![]() 所在直线对称,点D、E分别是AB、BC的中点,可得
所在直线对称,点D、E分别是AB、BC的中点,可得![]() =AC=2,∠B
=AC=2,∠B![]() C=∠A=90°,
C=∠A=90°,![]() B=AB,DE是△ABC的中位线,当
B=AB,DE是△ABC的中位线,当![]() 为直角三角形时,分情况讨论:①当∠
为直角三角形时,分情况讨论:①当∠![]() FE=90°时;②当∠
FE=90°时;②当∠![]() EF=90°时,分别画出图形计算即可得出答案.
EF=90°时,分别画出图形计算即可得出答案.
∵![]() 与
与![]() 关于
关于![]() 所在直线对称,点D、E分别是AB、BC的中点,
所在直线对称,点D、E分别是AB、BC的中点,
∴![]() =AC,∠B
=AC,∠B![]() C=∠A=90°,
C=∠A=90°,![]() B=AB,DE是△ABC的中位线,
B=AB,DE是△ABC的中位线,
当![]() 为直角三角形时,分情况讨论:
为直角三角形时,分情况讨论:
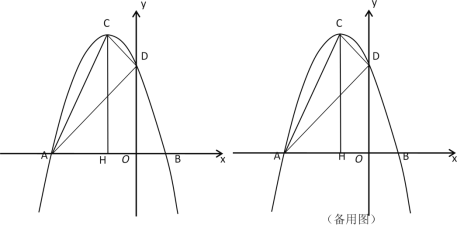
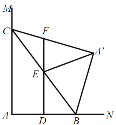
①当∠![]() FE=90°时,如图所示,DF∥AC,∠A=90°,
FE=90°时,如图所示,DF∥AC,∠A=90°,
∴DF⊥AB,DF⊥![]() C,
C,
∴![]() C∥AB,
C∥AB,
∴∠AC![]() =90°,即四边形AB
=90°,即四边形AB![]() C是矩形,
C是矩形,
又∵![]() B=AB,
B=AB,
∴矩形AB![]() C是正方形,
C是正方形,
∴AB=AC=2;
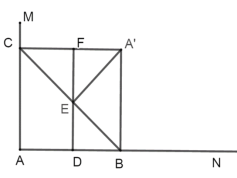
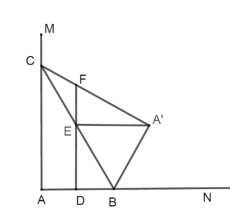
②当∠![]() EF=90°时,如图所示,
EF=90°时,如图所示,
∵![]() E∥AB,
E∥AB,![]() E=
E=![]() BC,
BC,
∴∠![]() EB=∠ABE=∠
EB=∠ABE=∠![]() BE,
BE,
∴![]() E=
E=![]() B=BE,
B=BE,
∴△![]() BE是等边三角形,∠
BE是等边三角形,∠![]() BE=60°,
BE=60°,
∵![]() C=AC=2,
C=AC=2,
∴![]() B=
B=![]() =
=![]() ,
,
∴AB=![]() ,
,
综上所述,AB的长度为2或![]() ,
,
故答案为:2或![]() .
.

练习册系列答案
相关题目