题目内容
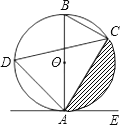
【题目】如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
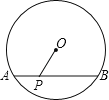
A.4个B.5个C.6个D.7个
【答案】D
【解析】
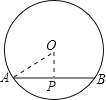
当P为AB的中点时OP最短,利用垂径定理得到OP垂直于AB,在直角三角形AOP中,由OA与AP的长,利用勾股定理求出OP的长;当P与A或B重合时,OP最长,求出OP的范围,由OP为整数,即可得到OP所有可能的长.
解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP=![]() =
=![]() =6,即OP的最小值为6;
=6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9
根据对称性可知,满足条件的点P的个数有7个
故选:D.

练习册系列答案
相关题目
【题目】体育理化考试前夕,九(2)班组织了体育理化考试模拟(体育+理化=100分),模拟测试后相关负责人对成绩进行了统计,制作如下频数分布表和频数分布直方图,请根据表中信息解答问题:
分数段( | 频数 | 频率 |
| 5 | 0.1 |
| 5 |
|
|
| 0.4 |
| 15 | 0.3 |
| 5 | 0.1 |
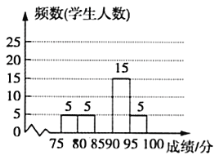
(1)表中![]() ________,
________,![]() ________,并补全直方图;
________,并补全直方图;
(2)若用扇形统计图描述此成绩分布情况,则分数段![]() 所对应扇形的圆心角度数是_____;
所对应扇形的圆心角度数是_____;
(3)若该校九年级共950名学生,请估计该年级分数在![]() 的学生有多少人?
的学生有多少人?