题目内容
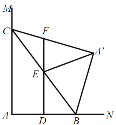
【题目】如图,在△ABC中,∠ACB=90°,AD=CD,点E在AB上,∠B=2∠AED,CF⊥ED,若CF=![]() ,BE+BC=
,BE+BC=![]() ,则EC=_____.
,则EC=_____.
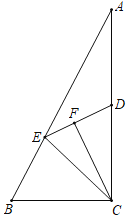
【答案】![]()
【解析】
如图,延长DE,CB交于点H,过点A作AN⊥DN,通过证明△CDF∽△HDC,可得![]() ,由勾股定理可求DF=2,CD=
,由勾股定理可求DF=2,CD=![]() ,由“AAS”可证△ADN≌△CDF,可得CF=AN=
,由“AAS”可证△ADN≌△CDF,可得CF=AN=![]() ,DF=DN=2,证明△AEN∽△DHC,由相似三角形的性质可求EN的长,由勾股定理可求解.
,DF=DN=2,证明△AEN∽△DHC,由相似三角形的性质可求EN的长,由勾股定理可求解.
解:如图,延长DE,CB交于点H,过点A作AN⊥DN,
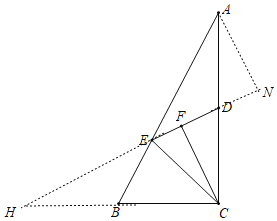
∵∠ABC=2∠AED,∠ABC=∠H+∠BEH=∠H+∠AED,
∴∠H=∠BEH,
∴BE=BH,
∴CH=BH+BC=BE+BC=![]() ,
,
∵∠CDF=∠CDH,∠ACB=∠CFD=90°,
∴△CDF∽△HDC,
∴![]() ,
,
设DF=![]() ,CD=
,CD=![]() ,
,
∵CD2=DF2+CF2,
∴a=![]() ,
,
∴DF=2,CD=![]() ,
,
∵AD=CD,∠ADN=∠CDF,∠N=∠CFD,
∴△ADN≌△CDF(AAS),
∴CF=AN=![]() ,DF=DN=2,
,DF=DN=2,
∵∠N=∠ACB,∠AEN=∠H,
∴△AEN∽△DHC,
∴![]() ,
,
∴![]() ,
,
∴EN=5,
∴EF=1,
∴EC=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
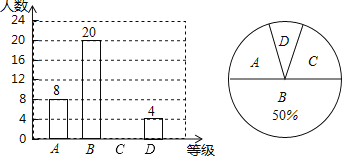
【题目】体育理化考试前夕,九(2)班组织了体育理化考试模拟(体育+理化=100分),模拟测试后相关负责人对成绩进行了统计,制作如下频数分布表和频数分布直方图,请根据表中信息解答问题:
分数段( | 频数 | 频率 |
| 5 | 0.1 |
| 5 |
|
|
| 0.4 |
| 15 | 0.3 |
| 5 | 0.1 |
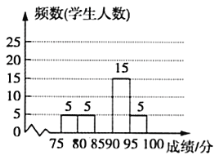
(1)表中![]() ________,
________,![]() ________,并补全直方图;
________,并补全直方图;
(2)若用扇形统计图描述此成绩分布情况,则分数段![]() 所对应扇形的圆心角度数是_____;
所对应扇形的圆心角度数是_____;
(3)若该校九年级共950名学生,请估计该年级分数在![]() 的学生有多少人?
的学生有多少人?