Question

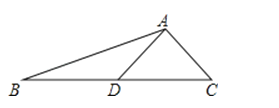
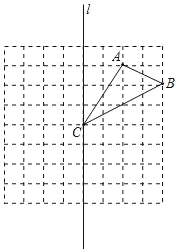
【题目】在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）．

(1)△ABC的面积为　 　；

(2)在直线l上找一点P，使点P到边AB、BC的距离相等．

(3)画出△ABC关于直线l对称的图形△A1B1C1；再将△A1B1C1向下平移4个单位，画出平移后得到的△A2B2C2．

(4)结合轴对称变换和平移变换的有关性质，两个对应三角形△ABC和△A2B2C2的对应点所具有的性质是（　 　）．

A．对应点连线与对称轴垂直 B．对应点连线被对称轴平分或与对称轴重合

C．对应点连线被对称轴垂直平分 D．对应点连线互相平行

Answer 1

【答案】(1)4；(2)见解析；(3)画图见解析；(4)B．

【解析】

（1）用一个矩形的面积分别减去三个三角形的面积可计算出△ABC的面积；

（2）作∠ABC的平分线交l于点P；

（3）利用对称的性质和平移的性质画出△A1B1C1和△A2B2C2；

（4）利用AA2和BB2被l平分，CC2在直线l上可对各选项进行判断．

（1）△ABC的面积=4×3﹣×4×2﹣×2×1﹣×2×3=4．

故答案为：4；

（2）如图，点P为所作；

（3）如图，△A1B1C1和△A2B2C2为所作；

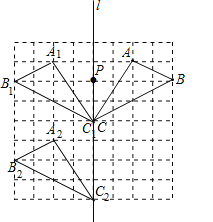
（4）对应点连线被对称轴平分或与对称轴重合．故选B．