题目内容
【题目】已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
A.∠AEB+22°=∠DEF
B.1+tan∠ADB=![]()
C.2BC=5CF
D.4cos∠AGB=![]()
【答案】B
【解析】解:如图,连接CE,设EF与BD相交于点O,
由轴对称性得,AB=AE,设为1,
则BE=![]() =
=![]() ,
,
∵点E与点F关于BD对称,
∴DE=BF=BE=![]() ,
,
∴AD=1+![]() ,
,
∵AD∥BC,AB⊥AD,AB=AE,
∴四边形ABCE是正方形,
∴BC=AB=1,∠AEB+22°=45°+22°=67°,
∵BE=BF,∠EBF=∠AEB=45°,
∴∠BFE=![]() =67.5°,
=67.5°,
∴∠DEF=∠BFE=67.5°,故A错误;
1+tan∠ADB=1+![]() =1+
=1+![]() ﹣1=
﹣1=![]() , 故B正确;
, 故B正确;
∵CF=BF﹣BC=![]() ﹣1,
﹣1,
∴5CF=5(![]() ﹣1),
﹣1),
又∵2BC=2×1=2,
∴2BC≠5CF,故C错误;
由勾股定理得,OE2=BE2﹣BO2=(![]() )2﹣(
)2﹣(![]() )2=
)2=![]() ,
,
∴OE=![]() ,
,
∵∠EBG+∠AGB=90°,∠EBG+∠BEF=90°,
∴∠AGB=∠BEF,
又∵∠BEF=∠DEF,
∴cos∠AGB=![]() =
=![]() =
=![]() , 4cos∠AGB=2
, 4cos∠AGB=2![]() , 故D错误.
, 故D错误.
故选:B.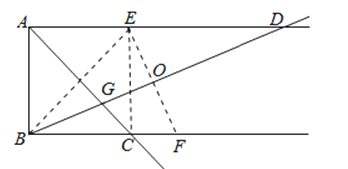
连接CE,设EF与BD相交于点O,根据轴对称性可得AB=AE,并设为1,利用勾股定理列式求出BE,再根据翻折的性质可得DE=BF=BE,再求出BC=1,然后对各选项分析判断利用排除法求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目