��Ŀ����
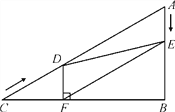
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��60 cm����A��60������D�ӵ�C������CA������4 cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2 cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��(0<t��15)������D��DF��BC�ڵ�F������DE��EF��
(1)��֤��AE��DF��
(2)�ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
(3)��tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
���𰸡�(1)֤����������(2) �ܣ����ɼ�������(3)��������
����������������1������t��ʾ��CD�Լ�AE�ij���Ȼ����ֱ�ǡ�CDF��������ֱ�������ε��������DF�ij�������֤����
��2����֤�ı���AEFD��ƽ���ı�������AD=AEʱ���ı���AEFD���������ݴ˼����з������t��ֵ��
��3��������������ۼ�����⣮
�������1����ֱ�ǡ�ABC������C=90�㩁��A=30�㣮
��CD=4t��AE=2t��
�֡���ֱ�ǡ�CDF������C=30�㣬��DF=![]() CD=2t����DF=AE��
CD=2t����DF=AE��
��2����DF��AB��DF=AE�����ı���AEFD��ƽ���ı�������AD=AEʱ���ı���AEFD����������60��4t=2t�������t=10������t=10ʱ��AEFD��������
��3�����������������
�ٵ���EDF=90��ʱ��DE��BC�����ADE=��C=30�㣬��AD=2AE��
��CD=4t����DF=2t=AE����AD=4t����4t+4t=60����t=![]() ʱ����EDF=90�㣮
ʱ����EDF=90�㣮
�ڵ���DEF=90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı�������AD��EF����DE��AD�����ADE��ֱ������������ADE=90�㣮
�ߡ�A=60�㣬���DEA=30�㣬��AD=![]() AE��AD=AC��CD=60��4t��AE=DF=
AE��AD=AC��CD=60��4t��AE=DF=![]() CD=2t����60��4t=t�����t=12��
CD=2t����60��4t=t�����t=12��
������������t=![]() ��t=12ʱ����DEF��ֱ�������Σ�
��t=12ʱ����DEF��ֱ�������Σ�

 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�