题目内容
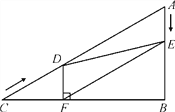
【题目】如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.

【答案】1或2.
【解析】试题分析:根据题意画出图形,过P作PN⊥BC,交BC于点N,
∵四边形ABCD为正方形,
∴AD=DC=PN,
在Rt△ADE中,∠DAE=30°,AD=3cm,
∴tan30°=![]() ,即DE=
,即DE=![]() cm,
cm,
根据勾股定理得:AE=![]() cm,
cm,
∵M为AE的中点,
∴AM=![]() cm;
cm;
在Rt△ADE和Rt△PNQ中,AD=PN,AE=PQ,
∴Rt△ADE≌Rt△PNQ(HL),
∴DE=NQ,∠DAE=∠NPQ=30°,
∵PN∥DC,
∴∠PFA=∠DEA=60°,
∴∠PMF=90°,即PM⊥AF,
在Rt△AMP中,∠MAP=30°,cos30°=![]() ,
,
∴AP=2cm;
由对称性得到AP′=DP=AD-AP=3-2=1cm,
综上,AP等于1cm或2cm.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目