题目内容
在三角形ABC中，∠A=30°，∠B=
∠C，则∠B=________．
60°
分析：根据三角形的内角和、已知条件知∠A+∠B+∠C=∠A+∠C+∠C=180°，从而求得∠C=90°，所以由∠B=∠C求得∠B=60°．
解答：
解：∵在三角形ABC中，∠A=30，∠B=∠C，
∴∠A+∠B+∠C=∠A+∠C+∠C=180°（三角形内角和定理），
又∵∠A=30°，
∴∠C=90°，
∴∠B=∠C=60°．
故答案是：60°．
点评：本题考查了三角形内角和定理．三角形的三个内角和是180°．
分析：根据三角形的内角和、已知条件知∠A+∠B+∠C=∠A+
∠C+∠C=180°，从而求得∠C=90°，所以由∠B=∠C求得∠B=60°．解答：
解：∵在三角形ABC中，∠A=30，∠B=∠C，∴∠A+∠B+∠C=∠A+
∠C+∠C=180°（三角形内角和定理），又∵∠A=30°，
∴∠C=90°，
∴∠B=
∠C=60°．故答案是：60°．
点评：本题考查了三角形内角和定理．三角形的三个内角和是180°．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
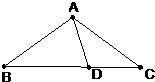22、如图，在三角形ABC中，AB=AC=BD，AD=CD，则∠B=
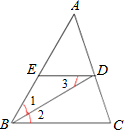20、如图，在三角形ABC中，BD平分∠ABC，∠1=∠3，求证：∠ADE=∠C．
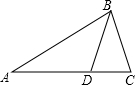如图，在三角形ABC中，若AB=AC，BD=BC，若∠ABD=30°，则∠A的大小是