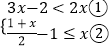Question

【题目】因为，所以．这说明能被整除，同时也说明多项式有一个因式为；另外，当多项式的值为．阅读上述材料回答问题：

（1）由可知，当_时，多项式的值为；

（2）一般地，如果一个关于字母的多项式当时，的值为，那么与代数式之间有一定的关系，这种关系是：_____；

（3）已知关于的多项式能被整除，试求的值．

Answer 1

【答案】（1）2或－1；（2）多项式M能被整除；（3）k的值为3

【解析】

（1）根据题意可知当因式或的值为0时，多项式的值为0，由此可得答案；

（2）当时，的值为，由此可判断是多项式M的一个因式；

（3）根据题意可知是多项式的一个因式，结合（1）（2）两问可知当时，，由此可得k的值．

解：（1）∵，

∴当或时，，

即：当或时，，

故答案为：2或－1；

（2）根据题意可知：是多项式M的一个因式，

故答案为：多项式M能被整除；

（3）根据题意可知：当时，，

即：当时，，

则，

解得，

答：k的值为3．