题目内容
【题目】在ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD= .
【答案】![]() 或5
或5
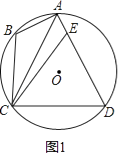
【解析】解:分两种情况:①如图1,
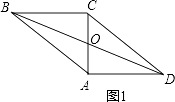
∵△ABC是直角三角形,
∠ACB=90°,AB=4,AC=3,
∴BC2=AB2﹣AC2=42﹣32=7.
∴AD=BC= ![]() ;②如图2,
;②如图2,
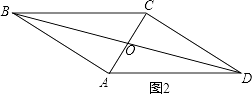
∵ABCD的对角线AC与BD相交于点O,
∴BD=2BO,OC=OA= ![]() AC,
AC,
∵∠BAC=90°,AB=4,AC=3,
∴BC2=AB2+AC2=16+9=25,
∴BC=5,
∴AD=5;
所以答案是: ![]() 或5.
或5.
【考点精析】根据题目的已知条件,利用勾股定理的概念和平行四边形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目