题目内容
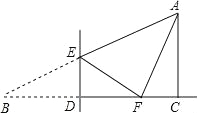
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 .
【答案】1或2
【解析】
试题分析:首先由在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,即可求得AC=BCtan∠B=3×![]() =
=![]() 、∠AEF=∠BAC=60°,然后分别从从∠AFE=90°与∠EAF=90°去分析求解:
、∠AEF=∠BAC=60°,然后分别从从∠AFE=90°与∠EAF=90°去分析求解:
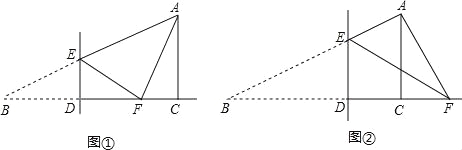
如图①若∠AFE=90°,
∵在Rt△ABC中,∠ACB=90°,
∴∠EFD+∠AFC=∠FAC+∠AFC=90°,
∴∠FAC=∠EFD=30°,
∴CF=ACtan∠FAC=![]() ×
×![]() =1,
=1,
∴BD=DF=![]() =1;
=1;
如图②若∠EAF=90°,
则∠FAC=90°﹣∠BAC=30°,
∴CF=ACtan∠FAC=![]() ×
×![]() =1,
=1,
∴BD=DF=![]() =2,
=2,
∴△AEF为直角三角形时,BD的长为:1或2.

练习册系列答案
相关题目
【题目】如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…

(1)完成下表:
连接个数 | ||||||
出现三角形个数 |
若出现了45个三角形,则共连接了多少个点?
若一直连接到An,则图中共有__________个三角形.