题目内容
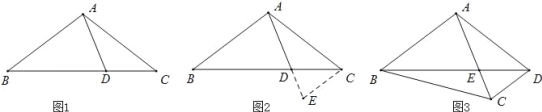
【题目】阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为 ,AC的长为 .
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
【答案】(1)3(2)∠ACE=75°,AC=3(3)![]()
【解析】
试题分析:根据相似的三角形的判定与性质,可得![]() =2,根据等腰三角形的判定,可得AE=AC,根据正切函数,可得DF的长,根据直角三角形的性质,可得AB与DF的关系,根据勾股定理,可得答案.
=2,根据等腰三角形的判定,可得AE=AC,根据正切函数,可得DF的长,根据直角三角形的性质,可得AB与DF的关系,根据勾股定理,可得答案.
试题解析:∠ABC+∠ACB=∠ECD+∠ACB=∠ACE=180°﹣75°﹣30°=75°,
∠E=75°,BD=2DC,
∴AD=2DE,
AE=AD+DE=3,
∴AC=AE=3,
∠ACE=75°,AC的长为3.
过点D作DF⊥AC于点F.
∵∠BAC=90°=∠DFA,
∴AB∥DF,
∴△ABE∽△FDE,
∴![]() =2,
=2,
∴EF=1,AB=2DF.
在△ACD中,∠CAD=30°,∠ADC=75°,
∴∠ACD=75°,AC=AD.
∵DF⊥AC,
∴∠AFD=90°,
在△AFD中,AF=2+1=3,∠FAD=30°,
∴DF=AFtan30°=![]() ,AD=2DF=2
,AD=2DF=2![]() .
.
∴AC=AD=2![]() ,AB=2DF=2
,AB=2DF=2![]() .
.
∴BC=![]() =
=![]() .
.


练习册系列答案
相关题目