题目内容
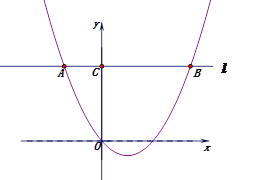
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1<m<n<1,则m+n<![]() ;④3|a|+|c|<2|b|.其中正确的结论个数是( )
;④3|a|+|c|<2|b|.其中正确的结论个数是( )
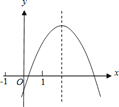
A. ①③④ B. ①③ C. ①④ D. ②③④
【答案】A
【解析】∵抛物线开口向下,∴a<0,∴2a<0,对称轴x=-![]() >1,-b<2a,∴2a+b>0,故①正确;
>1,-b<2a,∴2a+b>0,故①正确;
∵-b<2a,∴b>-2a>0>a,
令抛物线解析式为y=-![]() x 2 +bx-
x 2 +bx-![]() ,此时a=c,欲使抛物线与x轴交点的横坐标分别为
,此时a=c,欲使抛物线与x轴交点的横坐标分别为![]() 和2,则
和2,则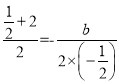 ,解得:b=
,解得:b=![]() ,
,
∴抛物线y=-![]() x 2 +
x 2 +![]() x-
x-![]() ,符合“开口向下,与x轴的一个交点的横坐标在0与1之间,
,符合“开口向下,与x轴的一个交点的横坐标在0与1之间,
对称轴在直线x=1右侧”的特点,而此时a=c,(其实a>c,a<c,a=c都有可能),故②错误;
∵-1<m<n<1,-2<m+n<2,
∴抛物线对称轴为:x=-![]() >1, -
>1, -![]() >2,m+n < -
>2,m+n < -![]() ,故③正确;
,故③正确;
当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,∴3a+c>-2b,∴-3a-c<2b,
∵a<0,b>0,c<0(图象与y轴交于负半轴),∴3|a|+|c|=-3a-c<2b=2|b|,故④正确.
故选A.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目