Question

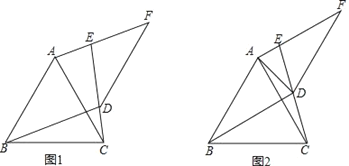
【题目】如图，正方形中，，是的中点.将沿对折至，延长交于点，连接、，则下列结论正确的有（ ）个.

（1） （2）

（3）的面积是18 （4）

A. 4B. 3C. 2D. 1

Answer 1

【答案】B

【解析】

①正确，根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE；在直角△ECG中，根据勾股定理即可求出DE的长；
②正确，根据翻折变换的性质和全等得出∠BAG=∠FAG，∠DAE=∠FAE，即可求出∠EAG=45°；

③错误，根据 即可求得结果；

④正确，作FM∥EC交BC于M，根据相似三角形的判定和性质 可得，求出FM和GM，根据勾股定理求得FC，即可解决问题．

解：①如图，连接AE，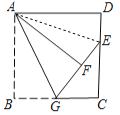

∵AB=AD=AF，∠D=∠AFE=90°，
在Rt△AFE和Rt△ADE中，
∵ ，
∴Rt△AFE≌Rt△ADE，
∴EF=DE，
设DE=FE=x，则EC=6-x．
∵G为BC中点，BC=6，
∴CG=3，
在Rt△ECG中，根据勾股定理，得：（6-x）2+9=（x+3）2，
解得x=2．故①正确；

②∵△ABG沿AG折叠得到△AFG，
∴△ABG≌△AFG．
∴∠BAG=∠FAG．
∵△ADE≌△AFE，
∴∠DAE=∠FAE．
∵∠BAD=90°，
∴∠EAG=∠EAF+∠GAF=×90°=45°．
故②正确；

③ ∵△ABG沿AG折叠得到△AFG，
∴△ABG≌△AFG．

∴AF=AB=6，∠AFG=∠B=90°，GF=BG=3，

∵ DE=FE=2，

∴ EG= GF+ FE=5,

∴= ，故③错误；

（4）作FM∥EC交BC于M，则∠FMC=∠DCM=90°，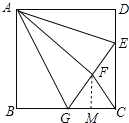

∵FM∥EC

∴△GMF∽△GCE，

∴ ，

∵G是BC的中点，BC=AB=6，

∴GC=3，

∵GF=3，GE=GF+EF=5，EC=CD-DE=4，

∴FM= ，GM= ，

∴MC= ，CF= = ，

∴ ，

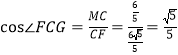故④正确.

故选：B．