题目内容
【题目】如图,双曲线![]() 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是_____.
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是_____.

【答案】3
【解析】
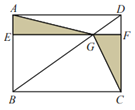
如图,延长BA交y轴于E,延长BC交x轴于F,连接OC.,由题意△ACB≌△ACB',△OCF≌△OCB',推出BC=CB'=CF,设BC=CF=a,OF=BE=2b,首先证明AE=AB,再证明S△ABC![]() S△OCF
S△OCF![]() ,由此即可解决问题.
,由此即可解决问题.
如图,延长BA交y轴于E,延长BC交x轴于F,连接OC.
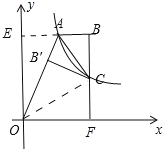
由题意△ACB≌△ACB',△OCF≌△OCB',∴BC=CB'=CF,设BC=CF=a,OF=BE=2b.
∵S△AOE=S△OCF,∴![]() 2a×AE
2a×AE![]() 2b×a,∴AE=b,∴AE=AB=b,∴S△ABC
2b×a,∴AE=b,∴AE=AB=b,∴S△ABC![]() S△OCF
S△OCF![]() ,S△OCB'=S△OFC=
,S△OCB'=S△OFC=![]() ,∴S四边形OABC=S△OCB'+2S△ABC
,∴S四边形OABC=S△OCB'+2S△ABC![]() 2
2![]() 3.
3.
故答案为:3.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
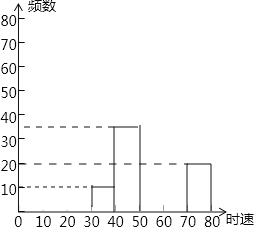
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a= ; b= ; c= ; d=
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?