题目内容
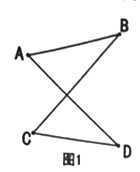
【题目】已知a、b、c在数轴上的位置如图所示,所对应的点分别为A、B、C,
![]()
(1)在数轴上表示2的点与表示5的点之间的距离为 ;
在数轴上表示﹣1的点与表示3的点之间的距离为 ;在数轴上表示﹣3的点与表示﹣5的点之间的距离为 ;由此可得点A、B之间的距离为 ,点B、C之间的距离为 ,点A、C之间的距离为 ;
(2)化简:﹣|a+b|+|c﹣b|﹣|b﹣a|;
(3)若c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣(a﹣4c﹣b)的值.
【答案】(1)3,4,2,a﹣b,b﹣c,a﹣c;(2)﹣13
【解析】
(1)根据两点间距离公式可得;
(2)结合数轴根据绝对值性质去绝对值符号,再合并即可得;
(3)根据a、b、c在数轴上的位置,结合题目条件得出c=-2,b=-1,a=2,再将其代入化简后的代数式即可
(1)5﹣2=3,3﹣(﹣1)=4,(3)﹣(﹣5)=2,A、B之间的距离为a﹣b,B、C之间的距离为b﹣c,A、C之间的距离为a﹣c,
故答案为;3,4,2,a﹣b,b﹣c,a﹣c;
(2)﹣|a+b|+|c﹣b|﹣|b﹣a|
=﹣(a+b)+(b﹣c)﹣(a﹣b)=﹣a﹣b+b﹣c﹣a+b=﹣2a+b﹣c;
(3)∵c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,
∴c=﹣2,b=﹣1,a=2,
∴﹣a+2b﹣c﹣(a﹣4c﹣b)=﹣2a+3b+3c=﹣13.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | … |
y | … |
|
|
|
| 3 |
|
|
| m | … |
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .