题目内容
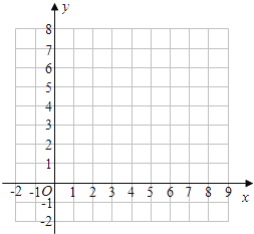
【题目】如图小方格的边长为1个单位。
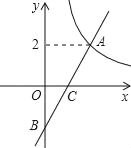
(1)画出坐标系，使A、B的坐标分别为(1,1)、(-2,0)，并写出点C的坐标；
(2)若将△ABC向右平移4个单位，再向上平移3个单位，得到
，在图中画出；
(3)写出△ABC的面积.
【答案】（1）C（-1,5）；（2）画图见解析；（3）三角形的面积为7
【解析】
（1）利用点A、B的坐标画出直角坐标系，然后写出C点坐标；
（2）利用点平移的坐标变换规律写出A′、B′、C′的坐标，然后描点即可得到△A′B′C′；
（3）用1个矩形的面积分别减去三个直角三角形的面积可计算出△ABC的面积．
解：（1）如图，点C的坐标为（-1，5）；
（2）如图，△A′B′C′为所作；
（3）△ABC的面积=3×5-
×3×1-×4×2-×5×1=7．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
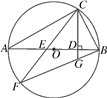
【题目】如图，已知AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，过点C作直线CD⊥AB于点D，点E是AB上一点，直线CE交⊙O于点F，连接BF与直线CD延长线交于点G.求证：BC2＝BG·BF.
【题目】已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：
△ABC | A（a，0） | B（3，0） | C（5，5） |
△A′B′C′ | A′（4，2） | B′（7，b） | C′（c，7） |
（1）观察表中各对应点坐标的变化，并填空：a=________，b=________，c=________；
（2）在平面直角坐标系中画出△ABC及平移后的△A′B′C′；
（3）直接写出△A′B′C′的面积是________．