题目内容
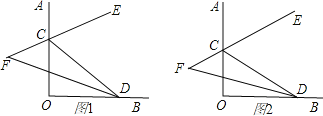
【题目】如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=50°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.
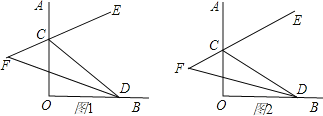
【答案】(1)∠F=45°;(2)不变化,∠F=45°.
【解析】
(1)根据三角形的内角和是180°,可求∠CDO=40°,所以∠CDF=20°,又由平角定义,可求∠ACD=130°,所以∠ECD=65°,又根据三角形的外角等于与它不相邻的两内角之和,可求∠ECD=∠F+∠CDF,∠F=45度.
(2)同理可证,∠F=45度.
(1)∵∠AOB=90°,∠OCD=50°,
∴∠CDO=40°.
∵CE是∠ACD的平分线,DF是∠CDO的平分线,
∴∠ECD=65°,∠CDF=20°.
∵∠ECD=∠F+∠CDF,
∴∠F=45°.
(2)不变化,∠F=45°.
∵∠AOB=90°,
∴∠CDO=90°-∠OCD,∠ACD=180°-∠OCD.
∵CE是∠ACD的平分线,DF是∠CDO的平分线,
∴∠ECD=90°-![]() ∠OCD,∠CDF=45°-
∠OCD,∠CDF=45°-![]() ∠OCD.
∠OCD.
∵∠ECD=∠F+∠CDF,
∴∠F=45°.

练习册系列答案
相关题目