Question

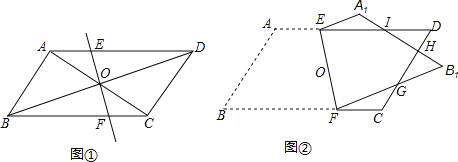
【题目】（1）如图①，ABCD的对角线AC，BD交于点O，直线EF过点O，分别交AD，BC于点E，F．求证：AE=CF．

（2）如图②，将ABCD（纸片）沿过对角线交点O的直线EF折叠，点A落在点A1处，点B落在点B1处，设FB1交CD于点G，A1B1分别交CD，DE于点H，I．求证：EI=FG．

Answer 1

【答案】（1）（2）证明见解析

【解析】

试题分析：（1）由四边形ABCD是平行四边形，可得AD∥BC，OA=OC，又由平行线的性质，可得∠1=∠2，继而利用ASA，即可证得△AOE≌△COF，则可证得AE=CF．

（2）根据平行四边形的性质与折叠性质，易得A1E=CF，∠A1=∠A=∠C，∠B1=∠B=∠D，继而可证得△A1IE≌△CGF，即可证得EI=FG．

证明：（1）∵四边形ABCD是平行四边形，

∴AD∥BC，OA=OC，

∴∠1=∠2，

∵在△AOE和△COF中，

，

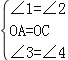∴△AOE≌△COF（ASA），

∴AE=CF；

（2）∵四边形ABCD是平行四边形，

∴∠A=∠C，∠B=∠D，

由（1）得AE=CF，

由折叠的性质可得：AE=A1E，∠A1=∠A，∠B1=∠B，

∴A1E=CF，∠A1=∠A=∠C，∠B1=∠B=∠D，

又∵∠1=∠2，

∴∠3=∠4，

∵∠5=∠3，∠4=∠6，

∴∠5=∠6，

∵在△A1IE与△CGF中，

，

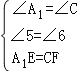∴△A1IE≌△CGF（AAS），

∴EI=FG．