Question

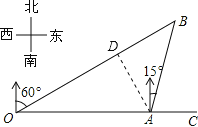
【题目】如图，港口A在观测站O的正东方向，OA=6km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（　　）

A. 3km B. 3km C. 4km D. （3-3）km

Answer 1

【答案】A

【解析】如图，如图，过点A作AD⊥OB于D．在Rt△AOD中，∠ADO=90°，∠AOD=30°，OA=6 km，根据在直角三角形中30°的锐角所对的直角边等于斜边的一半可得AD=3 km．在Rt△ABD中，∠ADB=90°，∠B=∠CAB-∠AOB=75°-30°=45°，根据等腰直角三角形的性质可得BD=AD=3 km，由勾股定理可得AB=3 km，即该船航行的距离（即AB的长）为3km．故选A．