题目内容
【题目】从A,B两题中任选一题作答:
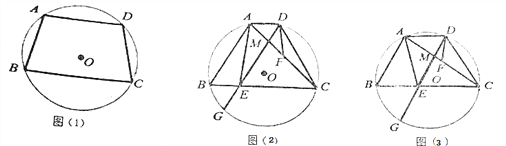
A.如图,在ΔABC中,分别以点A,B为圆心,大于![]() AB的长为半径画弧,两弧交与点M,N,作直线MN交AB于点E,交BC于点F,连接AF。若AF=6,FC=4,连接点E和AC的中点G,则EG的长为__.
AB的长为半径画弧,两弧交与点M,N,作直线MN交AB于点E,交BC于点F,连接AF。若AF=6,FC=4,连接点E和AC的中点G,则EG的长为__.

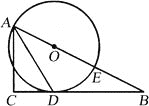
B.如图,在ΔABC中,AB=2,∠BAC=60°,点D是边BC的中点,点E在边AC上运动,当DE平分ΔABC的周长时,DE的长为__.

【答案】A.5 B.![]()
【解析】
A.由作法知MN是线段AB的垂直平分线,所以BF=AF=6,然后根据EG是三角形ABC的中位线求解即可;
B. 延长CA到点B′,使AB’等于AB,连接BB′,过点A作AF⊥BB′,垂足为F.由ED平分ΔABC的周长,可知EB′=EC,从而DE为ΔCBB′的中位线,由等腰三角形的性质求出∠B=∠B′=30°,从而BF=![]() ,进而可求出DE的长.
,进而可求出DE的长.
A.由尺规作图可得直线MN为线段AB的垂直平分线,
∴BF=AF=6,E为AB中点,
∵点G为AC中点,
∴EG为ΔABC的中位线,
∴EG∥BC且EG =![]() BC,
BC,
∵BF+FC=10,
∴EG=5;
B.如图所示,延长CA到点B′,使AB’等于AB,连接BB′,过点A作AF⊥BB′,垂足为F.
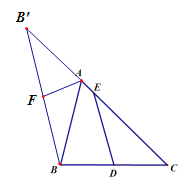
∵ED平分ΔABC的周长,∴AB+AE+BD=EC+DC.
∵BD=DC, ∴AB+AE=EC.
∵AB=AB′, ∴EB′=EC,
∴DE为ΔCBB′的中位线.
∵∠BAC=60°,
∴ΔBAB′为顶角是120°的等腰三角形 ,
∴∠B=∠B′=30°,
∴AF=1,
∴BF=![]() ,
,
∴BB′=2![]() ,
,
∴ED=![]() .
.
故答案为:A. 5;B![]() .
.

【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 80≤x<85 | 50 | 0.1 |
B | 85≤x<90 | 75 | |
C | 90≤x<95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?

【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.