题目内容
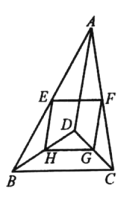
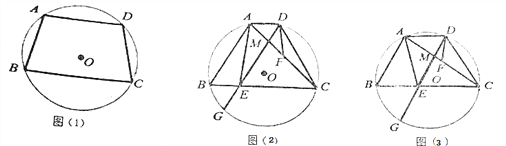
【题目】如图,四边形ABCD是⊙O的内接四边形,AB=CD.
(1)如图(1),求证:AD∥BC;
(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF;
(3)在(2)的条件下,若DG平分∠ADC,GE=5![]() ,tan∠ADF=4
,tan∠ADF=4![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接AC.由弦相等得到弧相等,进一步得到圆周角相等,即可得出结论.
(2)延长AD到N,使DN=AD,连接NC.得到四边形ABED是平行四边形,从而有AD=BE,DN=BE.由圆内接四边形的性质得到∠NDC=∠B.即可证明ΔABE≌ΔCND,得到AE=CN,再由三角形中位线的性质即可得出结论.
(3)连接BG,过点A作AH⊥BC,由(2)知∠AEB=∠ANC,四边形ABED是平行四边形,得到AB=DE.再证明ΔCDE是等边三角形,ΔBGE是等边三角形,通过解三角形ABE,得到AB,HB, AH,HE的长,由EC=DE=AB,得到HC的长.在Rt△AHC中,由勾股定理求出AC的长.
作直径AP,连接CP,通过解△APC即可得出结论.
试题解析:解:(1)连接AC.∵AB=CD,∴弧AB=弧CD,∴∠DAC=∠ACB,∴AD∥BC.

(2)延长AD到N,使DN=AD,连接NC.∵AD∥BC,DG∥AB,∴四边形ABED是平行四边形,∴AD=BE,∴DN=BE.∵ABCD是圆内接四边形,∴∠NDC=∠B.∵AB=CD,∴ΔABE≌ΔCND,∴AE=CN.∵DN=AD,AF=FC,∴DF=![]() CN,∴AE=2DF.
CN,∴AE=2DF.

(3)连接BG,过点A作AH⊥BC,由(2)知∠AEB=∠ANC,四边形ABED是平行四边形,∴AB=DE.
∵DF∥CN,∴∠ADF=∠ANC,∴∠AEB=∠ADF,∴tan∠AEB= tan∠ADF=![]() ,DG平分∠ADC,∴∠ADG=∠CDG.∵AD∥BC,∴∠ADG=∠CED,∠NDC=∠DCE.∵∠ABC=∠NDC,∴∠ABC=∠DCE.∵AB∥DG,∴∠ABC=∠DEC,∴∠DEC=∠ECD=∠EDC,∴ΔCDE是等边三角形,∴AB=DE=CE.∵∠GBC=∠GDC=60°,∠G=∠DCB=60°,∴ΔBGE是等边三角形,BE= GE=
,DG平分∠ADC,∴∠ADG=∠CDG.∵AD∥BC,∴∠ADG=∠CED,∠NDC=∠DCE.∵∠ABC=∠NDC,∴∠ABC=∠DCE.∵AB∥DG,∴∠ABC=∠DEC,∴∠DEC=∠ECD=∠EDC,∴ΔCDE是等边三角形,∴AB=DE=CE.∵∠GBC=∠GDC=60°,∠G=∠DCB=60°,∴ΔBGE是等边三角形,BE= GE=![]() .∵tan∠AEB= tan∠ADF=
.∵tan∠AEB= tan∠ADF=![]() ,设HE=x,则AH=
,设HE=x,则AH= ![]() .∵∠ABE=∠DEC=60°,∴∠BAH=30°,∴BH=4x,AB=8x,∴4x+x=
.∵∠ABE=∠DEC=60°,∴∠BAH=30°,∴BH=4x,AB=8x,∴4x+x=![]() ,解得:x=
,解得:x=![]() ,∴AB=8
,∴AB=8![]() ,HB=4
,HB=4![]() , AH=12,EC=DE=AB=
, AH=12,EC=DE=AB=![]() ,∴HC=HE+EC=
,∴HC=HE+EC=![]() =
=![]() .在Rt△AHC中,AC=
.在Rt△AHC中,AC=![]() =
=![]() .
.
作直径AP,连接CP,∴∠ACP=90°,∠P=∠ABC=60°,∴sin∠P=![]() ,∴
,∴ ,∴⊙O的半径是
,∴⊙O的半径是![]() .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案