题目内容
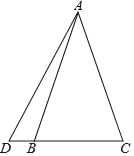
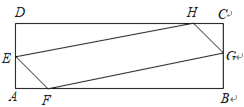
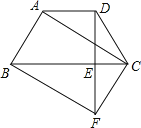
【题目】如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CD、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
【答案】 (1) 证明见解析;(2) 证明见解析.
【解析】
(1)连接BD,利用等腰梯形的性质得到AC=BD,再根据垂直平分线的性质得到DB=FB,从而得到AC=BF,然后证得AC∥BF,利用一组对边平行且相等判定平行四边形;(2)利用题目提供的等积式和两直角相等可以证得两直角三角形相似,得到对应角相等,从而得到直角来证明有一个角是直角的平行四边形是矩形.
(1)连接BD,
∵梯形ABCD中,AD∥BC,AB=CD,
∴AC=BD,
∵DE⊥BC,EF=DE,
∴BD=BF,CD=CF,
∴AC=BF,AB=CF,
∴四边形ABFC是平行四边形;
(2)∵DE2=BECE
∴![]() ,
,
∵∠DEB=∠DEC=90°,
∴△BDE∽△DCE,
∴∠CDE=∠DBE,
∴∠BFC=∠BDC=∠BDE+∠CDE=∠BDE+∠DBE=90°,
∴四边形ABFC是矩形.


 阅读快车系列答案
阅读快车系列答案【题目】今年4月份,某校九年级学生参加了广州市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
|
| 2 |
|
| 5 |
|
| 15 |
|
|
|
|
| 10 |
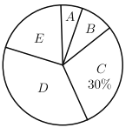
(1)求全班学生人数和![]() 的值.
的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图

根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.