题目内容
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
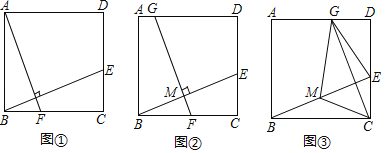
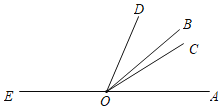
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
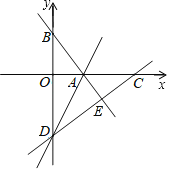
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
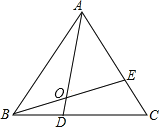
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
【答案】(1)证明见解析;(2)2,9.
【解析】感知:利用同角的余角相等判断出∠BAF=∠CBE,即可得出结论;
探究:(1)判断出PG=BC,同感知的方法判断出△PGF≌CBE,即可得出结论;
(2)利用直角三角形的斜边的中线是斜边的一半,
应用:借助感知得出结论和直角三角形斜边的中线是斜边的一半即可得出结论.
感知:∵四边形ABCD是正方形,
∴AB=BC,∠BCE=∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠BAF=∠CBE,
在△ABF和△BCE中,
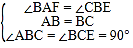 ,
,
∴△ABF≌△BCE(ASA);
探究:(1)如图②,
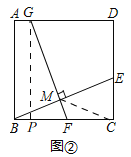
过点G作GP⊥BC于P,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
∴四边形ABPG是矩形,
∴PG=AB,∴PG=BC,
同感知的方法得,∠PGF=∠CBE,
在△PGF和△CBE中,
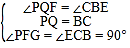 ,
,
∴△PGF≌△CBE(ASA),
∴BE=FG;
(2)由(1)知,FG=BE,
连接CM,
∵∠BCE=90°,点M是BE的中点,
∴BE=2CM=2,
∴FG=2,
故答案为:2.
应用:同探究(2)得,BE=2ME=2CM=6,
∴ME=3,
同探究(1)得,CG=BE=6,
∵BE⊥CG,
∴S四边形CEGM=![]() CG×ME=
CG×ME=![]() ×6×3=9,
×6×3=9,
故答案为:9.

【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收贵的价目表如下(注:水费按月份结算,![]() 表示立方米)
表示立方米)
价目表 | |
每月用水量 | 价格 |
不超过 |
|
超出 |
|
超出 |
|
![]() 某户居民1月份和2月份的用水量分别为
某户居民1月份和2月份的用水量分别为![]() 和
和![]() ,则应收水费分别是 元和 元
,则应收水费分别是 元和 元
![]() 若该户居民
若该户居民![]() 月份用水量
月份用水量![]() (其中
(其中![]() ),则应收水费多少元? (用含
),则应收水费多少元? (用含![]() 的式子表示,并化简)
的式子表示,并化简)
![]() 若该户居民
若该户居民![]() 两个月共用水
两个月共用水 ![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 两个月共交水费多少元? (用含
两个月共交水费多少元? (用含 ![]() 的式子表示,并化简)
的式子表示,并化简)