题目内容
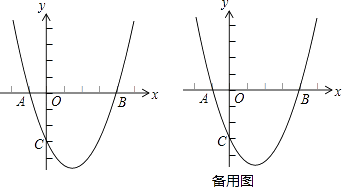
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.
【答案】
(1)
解:∵点B坐标为(4,0),抛物线的对称轴方程为x=1.
∴A(﹣2,0),
把点A(﹣2,0)、B(4,0)、点C(0,3),分别代入y=ax2+bx+c(a≠0),得
![]() ,解得
,解得  ,
,
所以该抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x+3
x+3
(2)
解:设运动时间为t秒,则AM=3t,BN=t.
∴MB=6﹣3t.
由题意得,点C的坐标为(0,3).
在Rt△BOC中,BC= ![]() =5.
=5.
如图1,过点N作NH⊥AB于点H.
∴NH∥CO,
∴△BHN∽△BOC,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴HN= ![]() t.
t.
∴S△MBN= ![]() MBHN=
MBHN= ![]() (6﹣3t)
(6﹣3t) ![]() t=﹣
t=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() ,
,
当△PBQ存在时,0<t<2,
∴当t=1时,
S△PBQ最大= ![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是 ![]()

(3)
解:如图2,
在Rt△OBC中,cos∠B= ![]() =
= ![]() .
.
设运动时间为t秒,则AM=3t,BN=t.
∴MB=6﹣3t.
当∠MNB=90°时,cos∠B= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
化简,得17t=24,解得t= ![]() ,
,
当∠BMN=90°时,cos∠B= ![]() =
= ![]() ,
,
化简,得19t=30,解得t= ![]() ,
,
综上所述:t= ![]() 或t=
或t= ![]() 时,△MBN为直角三角形.
时,△MBN为直角三角形.

【解析】(1)把点A、B、C的坐标分别代入抛物线解析式,列出关于系数a、b、c的解析式,通过解方程组求得它们的值;(2)设运动时间为t秒.利用三角形的面积公式列出S△MBN与t的函数关系式S△MBN=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() .利用二次函数的图象性质进行解答;(3)根据余弦函数,可得关于t的方程,解方程,可得答案.
.利用二次函数的图象性质进行解答;(3)根据余弦函数,可得关于t的方程,解方程,可得答案.

 天天练口算系列答案
天天练口算系列答案【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?