Question

【题目】已知等边△ABC的边长为12，D是AB上的动点，过D作DE⊥AC于点E，过E作EF⊥BC于点F，过F作FG⊥AB于点G．当G与D重合时，AD的长是（ ）
A.3
B.4
C.8
D.9

Answer 1

【答案】C
【解析】解：如图，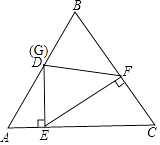
设BD=x，
∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°，
∵DE⊥AC于点E，EF⊥BC于点F，FG⊥AB，
∴∠BDF=∠DEA=∠EFC=90°，
∴BF=2x，
∴CF=12﹣2x，
∴CE=2CF=24﹣4x，
∴AE=12﹣CE=4x﹣12，
∴AD=2AE=8x﹣24，
∵AD+BD=AB，
∴8x﹣24+x=12，
∴x=4，
∴AD=8x﹣24=32﹣24=8．
故选C．
【考点精析】通过灵活运用等边三角形的性质和含30度角的直角三角形，掌握等边三角形的三个角都相等并且每个角都是60°；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半即可以解答此题．