题目内容
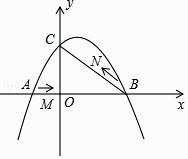
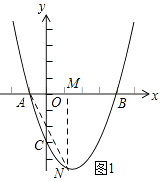
【题目】如图,抛物线y=ax2+bx﹣3经过A(﹣1,0)B(4,0)两点,与y轴交于点C
(1)求抛物线解析式;
(2)点N是x轴下方抛物线上的一点,连接AN,若tan∠BAN=2,求点N的纵坐标;
(3)点D是点C关于抛物线对称轴的对称点,连接AD,在x轴上是否存在E,使∠AED=∠CAD?如果存在,请直接写出点E坐标,如果不存在,请说明理由;
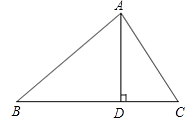
(4)连接AC、BC,△ABC的中线BM交y轴于点H,过点A作AG⊥BC,垂足为G,点F是线段BH上的一个动点(不与B、H重合),点F沿线段BH从点B向H移动,移动后的点记作点F′,连接F′C、F′A,△F′AC的F′C、F′A两边上的高交于点P,连接AP,CP,△F′AC与△PAC的面积分别记为S1 , S2 , S1和S2的乘积记为m,在点F的移动过程中,探究m的值变化情况,若变化,请直接写出m的变化范围,若不变,直接写出这个m值.
【答案】
(1)
解:将点A和点B的坐标代入抛物线的解析式得: ![]() ,
,
解得: 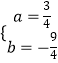 .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣3.
x﹣3.
(2)
如图1所示:过点N作NM⊥x轴点M,则∠AMN=90°.
设点N的坐标为(x, ![]() x2﹣
x2﹣ ![]() x﹣3),则AM=x+1,MN=﹣
x﹣3),则AM=x+1,MN=﹣ ![]() x2+
x2+ ![]() x+3.
x+3.
∵tan∠BAN=2,
∴ ![]() =2,解得:x=
=2,解得:x= ![]() 或x=﹣1(舍去).
或x=﹣1(舍去).
∴MN=2AM=3×( ![]() +1)=
+1)= ![]() ,
,
∴点N的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
(3)
如图2所示:连接CD,过点C作CG⊥AD,垂足为G,过点D作DF⊥x轴,垂足为F.

∵点C与点D关于对称轴直线x= ![]() 对称,
对称,
∴D(3,﹣3).
∴DF=3,CD=3.
依据两点间的距离公式可知AD=5,AC= ![]() .
.
∵S△ACD= ![]() CDOC=
CDOC= ![]() ADCG,
ADCG,
∴CG= ![]() .
.
∴AG= ![]() =
= ![]() .
.
∴tan∠CAD= ![]() .
.
∵∠AED=∠CAD,
∴tan∠AED= ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得EF=EF′=
,解得EF=EF′= ![]() .
.
∴E(﹣ ![]() ,0),E′(
,0),E′( ![]() ,0).
,0).
∴点E的坐标为(﹣ ![]() ,0)或(
,0)或( ![]() ,0).
,0).
(4)
如图3所示:
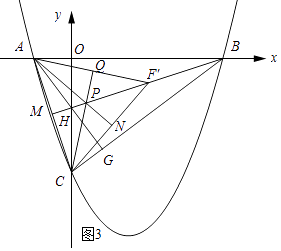
∵A(﹣1,0),(4,0),C(0,﹣3),
∴AB=BC=5,AC= ![]() .
.
∵MB为△ABC的中线,
∴MB⊥AC,MC= ![]() .
.
∴MB为AC的垂直平分线,
∴∠AF′M=∠CF′M.
∵点P为AF′与CF′的高线的交点,
∴∠CAQ+∠ACQ=90°,∠CAQ+∠MF′A=90°,
∴∠ACQ=∠AF′M.
∴∠ACQ=∠CF′M.
又∵∠CMP=∠CMF′,
∴△CMP∽△F′MC.
∴ ![]() =
= ![]() ,即MPMF′=
,即MPMF′= ![]() .
.
∴m=S1S2= ![]() ACPM
ACPM ![]() ACMF′=
ACMF′= ![]() ×(
×( ![]() )2×
)2× ![]() =
= ![]() .
.
【解析】(1)将点A和点B的坐标代入抛物线的解析式得到关于a、b的方程组,然后求得a、b的值即可;(2)过点N作NM⊥x轴点M,则∠AMN=90°.设点N的坐标为(x, ![]() x2﹣
x2﹣ ![]() x﹣3),则AM=x+1,MN=﹣
x﹣3),则AM=x+1,MN=﹣ ![]() x2+
x2+ ![]() x+3,然后依据tan∠BAN=2,列方程求解即可;(3)连接CD,过点C作CG⊥AD,垂足为G,过点D作DF⊥x轴,垂足为F.先求得AC,AD的长,依据S△ACD=
x+3,然后依据tan∠BAN=2,列方程求解即可;(3)连接CD,过点C作CG⊥AD,垂足为G,过点D作DF⊥x轴,垂足为F.先求得AC,AD的长,依据S△ACD= ![]() CDOC=
CDOC= ![]() ADCG,可求得CG的长,然后依据勾股定理可求得AG的长,从而可得到tan∠AED=
ADCG,可求得CG的长,然后依据勾股定理可求得AG的长,从而可得到tan∠AED= ![]() =
= ![]() =
= ![]() ,从而可求得EF和E′F的长,然后求得点E和点E′的坐标即可;(4)先证明AB=BC,由等腰三角形的性质可知MB为AC的垂直平分线,然后再证明△CMP∽△F′MC,依据相似三角形的性质可求得MPMF′=
,从而可求得EF和E′F的长,然后求得点E和点E′的坐标即可;(4)先证明AB=BC,由等腰三角形的性质可知MB为AC的垂直平分线,然后再证明△CMP∽△F′MC,依据相似三角形的性质可求得MPMF′= ![]() ,最后由m=S1S2=
,最后由m=S1S2= ![]() ACPM
ACPM ![]() ACMF′求解即可.
ACMF′求解即可.
【考点精析】解答此题的关键在于理解锐角三角函数的定义的相关知识,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了创建书香校园,切实引导学生多读书,读好书.某中学开展了“好书伴我成长”的读书节活动,为了了解本校学生每周课外阅读时间,随机抽取部分学生进行问卷调查,将课外阅读时间分为A、B、C、D四组,并利用臭氧所得的数据绘制了如下统计图.
组别 | 课外阅读t(单位:时) |
A | X<2 |
B | 2≤x<3 |
C | 3≤x<4 |
D | x≥4 |
请根据图中提供的信息,解答下列问题:
(1)一共调查了名学生;
(2)扇形统计图中A组的圆心角度数;
(3)直接补全条形统计图
(4)若该校有2400名学生,根据你所调查的结果,估计每周课外阅读时间不足3小时的学生有多少人?