题目内容
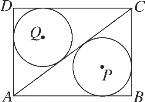
【题目】如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据矩形的性质可得出⊙P和⊙Q的半径相等,利用直角三角形内切圆半径公式即可求出⊙P半径r的长度.连接点P、Q,过点Q作QE∥BC,过点P作PE∥AB交QE于点E,求出线段QE、EP的长,再由勾股定理即可求出线段PQ的长,此题得解.
解:∵四边形ABCD为矩形,
∴△ACD≌△CAB,
∴⊙P和⊙Q的半径相等.
在Rt△ABC中,AB=4,BC=3,
∴AC=![]() =5,
=5,
∴⊙P的半径r=![]()
=![]() =1.
=1.
连接点P、Q,过点Q作QE∥BC,过点P作PE∥AB交QE于点E,则∠QEP=90°,如图所示.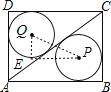
在Rt△QEP中,QE=BC-2r=3-2=1,EP=AB-2r=4-2=2,
∴PQ=![]()
=![]() =
=![]() .
.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目