题目内容
【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

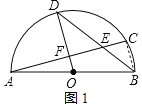
(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
【答案】(1)AC=![]() ;(2)cot∠ABD=
;(2)cot∠ABD=![]() ;(3)S△ACD=
;(3)S△ACD=![]() .
.
【解析】(1)由AC=BD知![]() ,得
,得![]() ,根据OD⊥AC知
,根据OD⊥AC知![]() ,从而得
,从而得![]() ,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
(2)连接BC,设OF=t,证OF为△ABC中位线及△DEF≌△BEC得BC=DF=2t,由DF=1﹣t可得t=![]() ,即可知BC=DF=
,即可知BC=DF=![]() ,继而求得EF=
,继而求得EF=![]() AC=
AC=![]() ,由余切函数定义可得答案;
,由余切函数定义可得答案;
(3)先求出BC、CD、AD所对圆心角度数,从而求得BC=AD=![]() 、OF=
、OF=![]() ,从而根据三角形面积公式计算可得.
,从而根据三角形面积公式计算可得.
(1)∵OD⊥AC,
∴![]() ,∠AFO=90°,
,∠AFO=90°,
又∵AC=BD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=2,
∴AO=BO=1,
∴AF=AOsin∠AOF=1×![]() =
=![]() ,
,
则AC=2AF=![]() ;
;
(2)如图1,连接BC,
∵AB为直径,OD⊥AC,
∴∠AFO=∠C=90°,
∴OD∥BC,
∴∠D=∠EBC,
∵DE=BE、∠DEF=∠BEC,
∴△DEF≌△BEC(ASA),
∴BC=DF、EC=EF,
又∵AO=OB,
∴OF是△ABC的中位线,
设OF=t,则BC=DF=2t,
∵DF=DO﹣OF=1﹣t,
∴1﹣t=2t,
解得:t=![]() ,
,
则DF=BC=![]() 、AC=
、AC=![]() =
=![]() ,
,
∴EF=![]() FC=
FC=![]() AC=
AC=![]() ,
,
∵OB=OD,
∴∠ABD=∠D,
则cot∠ABD=cot∠D=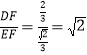 ;
;
(3)如图2,
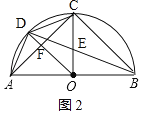
∵BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,
∴∠BOC=![]() 、∠AOD=∠COD=
、∠AOD=∠COD=![]() ,
,
则![]() +2×
+2×![]() =180,
=180,
解得:n=4,
∴∠BOC=90°、∠AOD=∠COD=45°,
∴BC=AC=![]() ,
,
∵∠AFO=90°,
∴OF=AOcos∠AOF=![]() ,
,
则DF=OD﹣OF=1﹣![]() ,
,
∴S△ACD=![]() ACDF=
ACDF=![]() ×
×![]() ×(1﹣
×(1﹣![]() )=
)=![]() .
.