题目内容
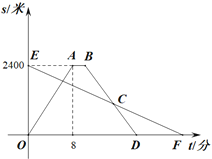
【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
(1)求s1与t之间的函数表达式;
(2)小明从家出发,经过_______分在返回途中追上爸爸.
【答案】(1)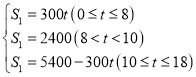 (2)15
(2)15
【解析】
(1)先根据图象可知:A(8,2400);B(10,2400);D(18,0),分3段列出解析式即可;
(2)根据E、F点的坐标求出EF所在的直线方程,求由BD与EF所在直线的交点即根据S1=S2列出方程求解即可.
解:(1)根据题意和图象可知:A(8,2400);B(10,2400);D(18,0),
当0≤t≤8时,设S1=kt,k=300,∴S1=300t;
当8<t<10时,S1=2400;
当10≤t≤18时,设S1=k1t+b,
将B、D点坐标代入得: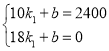
解得:![]()
∴S1=5400-300t
∴s1与t之间的函数表达式为: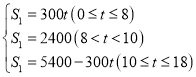
(2)∵2400÷100=24
∴点F的坐标为:(24,0)
设S2与t之间的函数表达式是S2=kt+b,则
![]() 解得:
解得:![]()
即S2与t之间的函数表达式是:S2=2400-100 t
根据题意列方程得:![]() ,
,
解得:t=15
∴小明从家出发,经过15分钟在返回途中追上爸爸.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目