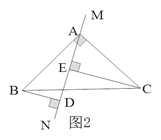题目内容
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】试题分析:①利用等边对等角,即可证得∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此可以求解;②证明∠POC=60°,且OP=OC,即可证得△OPC是等边三角形;③首先证明,△POA≌△CPE,则AO=CE,AC=AE+CE=AO+AP;④过带你C做CH⊥AB于H,根据S四边形AOCP=S△ACP+S△AOC,利用三角形的面积公式即可求解.所以4个结论都正确.
故选D.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目