题目内容
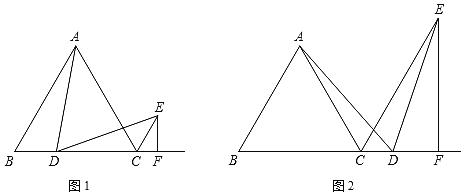
【题目】已知:在△ABC中，且∠BAC＝70°，AD是△ABC的角平分线，点E是AC边上的一点，点F为直线AB上的一动点，连结EF，直线EF与直线AD交于点P，设∠AEF＝α°
(1)如图①，若 DE//AB，则①∠ADE的度数是_______;
②当∠DPE＝∠DEP时，∠AEF= _____度:当∠PDE＝∠PED，∠AEF=_______度;
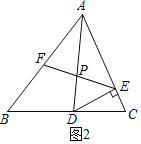
(2)如图②，若DE⊥AC，则是否存在这样的α的值，使得△DPE中有两个相等的角?若存在求出α的值;若不存在，说明理由
【答案】（1）①35°；②37.5，75；（2）27.5°或20°或35°．
【解析】
（1）①利用平行线的性质，可知∠ADE=∠BAD，由此即可解决问题；
②利用三角形的内角和定理以及三角形的外角的性质解决问题即可；
（2）用分类讨论的思想思考问题即可；
解：（1）①∵∠BAC=70°，AD是△ABC的角平分线，
∴∠BAD=
∠BAC=35°，
∵DE∥AB，
∴∠ADE=∠BAD=35°，
故答案为35°．
②在△DPE中，∵∠ADE=35°，
∴∠DPE=∠PED=（180°-35°）=72.5°，
∵∠DPE=∠AEP+∠DAE，
∴∠AEF=72.5°-35°=37.5°；
∵当∠PDE=∠PED时，∠DPE=70°，
∴∠AEF=∠DPE-∠DAE=75°．
故答案为37.5，75；
（2）在Rt△ADE中，∠ADE=90°-35°=55°．
①当DP=DE时，∠DPE=62.5°，∠AEF=∠DPE-∠DAC=62.5°-35°=27.5°．
②当EP=ED时，∠EPD=∠ADE=55°，∠AEF=∠DPE-∠DAC=55°-35°=20°．
③当DP=PE时，∠EPD=180°-2×55°=70°，∠AEF=∠DPE-∠DAC=70°-35°=35°．
