题目内容
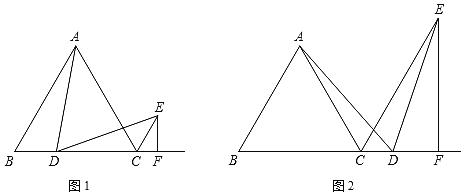
【题目】在等边△ABC中,D为射线BC上一点,CE是∠ACB外角的平分线,∠ADE=60°,EF⊥BC于F.
(1)如图1,若点D在线段BC上,证明:∠BAD=∠EDC;
(2)如图1,若点D在线段BC上,证明:①AD=DE;②BC=DC+2CF(提示:构造全等三角形);
(3)如图2,若点D在线段BC的延长线上,直接写出BC、DC、CF三条线段之间的数量关系.
【答案】(1)见解析;(2)①见解析;②见解析;(3)BC=2CF-DC;理由见解析.
【解析】
(1)由等边三角形的性质得出∠B=60°,再由三角形的外角性质结合已知条件,即可得出结论;
(2)过D作DG∥AC交AB延长线于G,证得△AGD≌△DCE,得出:①AD=DE;进一步利用GD=CE,BD=CE得出②BC=DC+2CF;
(3)过D作DG∥AC交AB延长线于G,由平行线和等边三角形的性质得出∠BGD=∠BDG=∠B=60°,证出△GBD是等边三角形,证出AG=CD,再证出∠GAD=∠CDE,证明△AGD≌△DCE,得出GD=CE,进而得出结论.
(1)∵△ABC是等边三角形,
∴∠B=60°,
∵∠ADC=∠ADE+∠EDC=∠B+∠BAD,∠ADE=60°,
∴∠BAD=∠EDC;
(2)①过D作DG∥AC交AB于G,如图1所示:

∵△ABC是等边三角形,AB=BC,
∴∠B=∠ACB=60°,
∴∠BDG=∠ACB=60°,
∴∠BGD=60°,
∴△BDG是等边三角形,
∴BG=BD,∠AGD=∠B+∠BDG=60°+60°=120°,
∴AG=DC,
∵CE是∠ACB外角的平分线,
∴∠DCE=120°=∠AGD,
由(1)知∠GAD=∠EDC,
在△AGD和△DCE中,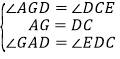 ,
,
∴△AGD≌△DCE(ASA),
∴AD=DE;
②∵△AGD≌△DCE,
∴GD=CE,
∴BD=CE,
∵EF⊥BC,CE是∠ACB外角的平分线,
∴∠ECF=60°,∠CEF=30°,
∴CE=2CF,
∴BC=CE+DC=DC+2CF;
(3)BC=2CF-DC;理由如下:
过D作DG∥AC交AB延长线于G,如图2所示:
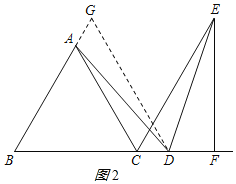
∵DG∥AC,△ABC是等边三角形,
∴∠BGD=∠BDG=∠B=60°,
∴△GBD是等边三角形,
∴GB-AB=DB-BC,即AG=DC,
∵∠ACB=60,CE是∠ACB的外角平分线,
∴∠DCE=∠ACE=![]() ×(180°-∠ACB)=60°,
×(180°-∠ACB)=60°,
∴∠AGD=∠DCE=60°,
∵∠GAD=∠B+∠ADC=60°+∠ADC,
∠CDE=∠ADC+∠ADE=∠ADC+60°,
∴∠GAD=∠CDE,
在△AGD和△DCE中,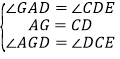 ,
,
∴△AGD≌△DCE(ASA),
∴GD=CE,
∴BD=CE,
∵CE=2CF,
∴BC=BD-DC=CE-DC=2CF-DC.