ЬтФПФкШн
ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПЭЌвЛЦНУцжБНЧзјБъЯЕжаЯЕЪ§ЛЅЮЊЕЙЪ§ЕФе§ЁЂЗДБШР§КЏЪ§![]() гы
гы![]() ЃЈkЁй0ЃЉЕФЭМЯѓаджЪЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓаджЪЃЎ
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() гы
гы![]() ЃЈkЁй0ЃЉЃЌЕБkЃО0ЪБЕФЭМЯѓаджЪНјааСЫЬНОПЃЎ
ЃЈkЁй0ЃЉЃЌЕБkЃО0ЪБЕФЭМЯѓаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃК
ЃЈ1ЃЉШчЭМЫљЪОЃЌЩшКЏЪ§![]() гы
гы![]() ЭМЯѓЕФНЛЕуЮЊAЁЂBЃЌвбжЊAЕуЕФзјБъЮЊЃЈЉkЃЌЉ1ЃЉЃЌдђBЕуЕФзјБъЮЊЁЁ ЁЁЃЛ
ЭМЯѓЕФНЛЕуЮЊAЁЂBЃЌвбжЊAЕуЕФзјБъЮЊЃЈЉkЃЌЉ1ЃЉЃЌдђBЕуЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЕуPЮЊЕквЛЯѓЯоФкЫЋЧњЯпЩЯВЛЭЌгкЕуBЕФШЮвтвЛЕуЃЎ
ЂйЩшжБЯпPAНЛxжсгкЕуMЃЌжБЯпPBНЛxжсгкЕуNЃЎЧѓжЄЃКPM=PNЃЎ
жЄУїЙ§ГЬШчЯТЃЌЩшPЃЈmЃЌ![]() ЃЉЃЌжБЯпPAЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
ЃЉЃЌжБЯпPAЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
дђ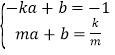 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпPAЕФНтЮіЪНЮЊЁЁ ЁЁ.
ЧыФуАбЩЯУцЕФНтД№Й§ГЬВЙГфЭъећЃЌВЂЭъГЩЪЃгрЕФжЄУїЃЎ
ЂкЕБPЕузјБъЮЊЃЈ1ЃЌkЃЉЃЈkЁй1ЃЉЪБЃЌХаЖЯЁїPABЕФаЮзДЃЌВЂгУkБэЪОГіЁїPABЕФУцЛ§ЃЎ
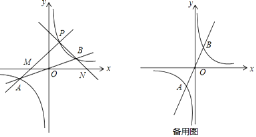
ЁОД№АИЁП(1) BЃЈkЃЌ1ЃЉ;(2)ЂйМћНтЮі;Ђк1Љk2.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОне§ЁЂЗДБШР§КЏЪ§ЭМЯѓЕФЖдГЦадНсКЯЕуAЕФзјБъМДПЩЕУГіЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЂйЩш![]() ЃЌИљОнЕуPЁЂAЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіжБЯпPAЕФНтЮіЪНЃЌРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуMЕФзјБъЃЌЙ§ЕуPзїPHЁЭxжсгкHЃЌгЩЕуPЕФзјБъПЩЕУГіЕуHЕФзјБъЃЌНјЖјМДПЩЧѓГіMHЕФГЄЖШЃЌЭЌРэПЩЕУГіHNЕФГЄЖШЃЌдйИљОнЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛМДПЩжЄГіPM=PNЃЛ
ЃЌИљОнЕуPЁЂAЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіжБЯпPAЕФНтЮіЪНЃЌРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуMЕФзјБъЃЌЙ§ЕуPзїPHЁЭxжсгкHЃЌгЩЕуPЕФзјБъПЩЕУГіЕуHЕФзјБъЃЌНјЖјМДПЩЧѓГіMHЕФГЄЖШЃЌЭЌРэПЩЕУГіHNЕФГЄЖШЃЌдйИљОнЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛМДПЩжЄГіPM=PNЃЛ
ЂкИљОнЂйНсКЯPHЁЂMHЁЂNHЕФГЄЖШЃЌПЩЕУГіЁїPABЮЊжБНЧШ§НЧаЮЃЌЗжk>1КЭ0<k<1СНжжЧщПіЃЌРћгУЗжИюЭМаЮЧѓУцЛ§ЗЈМДПЩЧѓГіЁїPABЕФУцЛ§ЃЎ
(1)гЩе§ЁЂЗДБШР§КЏЪ§ЭМЯѓЕФЖдГЦадПЩжЊЃЌЕуA. BЙигкдЕуOЖдГЦЃЌ
ЁпAЕуЕФзјБъЮЊ(k,1)ЃЌ
ЁрBЕуЕФзјБъЮЊ(k,1).
ЙЪД№АИЮЊЃК(k,1).
ЃЈ2ЃЉ)ЂйжЄУїЙ§ГЬШчЯТ,Щш![]() ,жБЯпPAЕФНтЮіЪНЮЊy=ax+b(aЁй0).
,жБЯпPAЕФНтЮіЪНЮЊy=ax+b(aЁй0).
дђ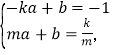
НтЕУЃК 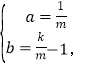
ЁржБЯпPAЕФНтЮіЪНЮЊ![]()
ЕБy=0ЪБЃЌx=mkЃЌ
ЁрMЕуЕФзјБъЮЊ(mk,0).
Й§ЕуPзїPHЁЭxжсгкHЃЌШчЭМ1ЫљЪОЃЌ
ЁпPЕузјБъЮЊ![]() ЃЌ
ЃЌ
ЁрHЕуЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌ
ЁрMH=xHЉxM=mЉЃЈmЉkЃЉ=kЃЎ
ЭЌРэПЩЕУЃКHN=kЃЎ
ЁрMH=HNЃЌЁрPM=PNЃЎ
ЂкгЩЂйПЩжЊЃЌдкЁїPMNжаЃЌPM=PNЃЌЁрЁїPMNЮЊЕШбќШ§НЧаЮЃЌЧвMH=HN=kЃЎ
ЕБPЕузјБъЮЊЃЈ1ЃЌkЃЉЪБЃЌPH=kЃЌЁрMH=HN=PHЃЌ
ЁрЁЯPMH=ЁЯMPH=45ЁуЃЌЁЯPNH=ЁЯNPH=45ЁуЃЌ
ЁрЁЯMPN=90ЁуЃЌМДЁЯAPB=90ЁуЃЌЁрЁїPABЮЊжБНЧШ§НЧаЮЃЎ
ЕБkЃО1ЪБЃЌШчЭМ1ЃЌ
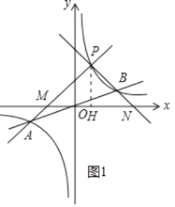
SЁїPAB=SЁїPMNЉSЁїOBN+SЁїOAMЃЌ
=![]() MNPHЉ
MNPHЉ![]() ONyB+
ONyB+![]() OM|yA|ЃЌ
OM|yA|ЃЌ
=![]() ЁС2kЁСkЉ
ЁС2kЁСkЉ![]() ЃЈk+1ЃЉЁС1+
ЃЈk+1ЃЉЁС1+![]() ЃЈkЉ1ЃЉЁС1ЃЌ
ЃЈkЉ1ЃЉЁС1ЃЌ
=k2Љ1ЃЛ
ЕБ0ЃМkЃМ1ЪБЃЌШчЭМ2ЃЌ
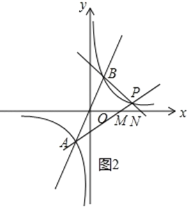
SЁїPAB=SЁїOBNЉSЁїPMN+SЁїOAMЃЌ
=![]() ONyBЉk2+
ONyBЉk2+![]() OM|yA|ЃЌ
OM|yA|ЃЌ
=![]() ЃЈk+1ЃЉЁС1Љk2+
ЃЈk+1ЃЉЁС1Љk2+![]() ЃЈ1ЉkЃЉЁС1ЃЌ
ЃЈ1ЉkЃЉЁС1ЃЌ
=1Љk2ЃЎ

 ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ
ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ ЦЗбЇЫЋгХОэЯЕСаД№АИ
ЦЗбЇЫЋгХОэЯЕСаД№АИ






