题目内容
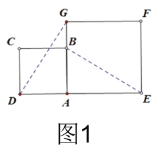
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明理由)
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明理由)
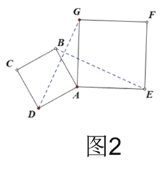
(1)如图2,小明将正方形ABCD绕点A逆时针旋转,旋转角为![]() (30﹤
(30﹤![]() ﹤180)
﹤180)
①连接DG,BE,求证:DG=BE且DG⊥BE;
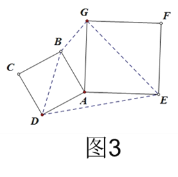
②在旋转过程中,如图3,连接BG,GE,ED,DB,求出四边形BGED面积的最大值.
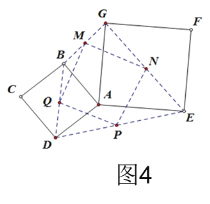
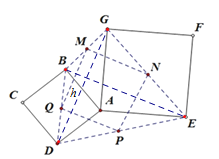
(2)如图4,分别取BG,GE,ED,DB的中点M,N,P,Q,连接MN,NP,PQ,QM,则四边形MNPQ的形状为 ,四边形MNPQ面积的最大值是 ,
【答案】(1)①证明见解析;②四边形BGED面积的最大值为6+4![]() ;(2)正方形,3+2
;(2)正方形,3+2![]() .
.
【解析】
(1)①由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应角相等得DG=BE,∠AGD=∠AEB,如图所示,EB交AG于点H,利用等角的余角相等得到∠GMH =90°,利用垂直的定义即可得DG⊥BE;
②根据①可知旋转过程中,DG=BE且DG⊥BE;当BE取得最大值,即点A,B,E在同一条直线上时,四边形BGED面积有最大值.
(2)根据中点四边形的性质可知四边形MNPQ是正方形,边长的最大值为![]()
四边形MNPQ面积的最大值是:![]()
(1) ①∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAB=∠GAE=![]() ,AG=AE,
,AG=AE,
∠DAB+∠GAB=∠GAB +∠GAE
∠DAG=∠BAE
在△ADG和△ABE中,
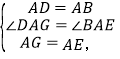 ∴△ADG≌△ABE(SAS),
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,DG=BE,
如图所示,EB交AG于点H,
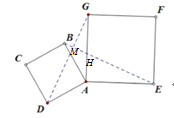
在△AEH中,∠AEH+∠AHE=![]() ,
,
∠AEH=∠BHG,
∴∠AGD+∠BHG=![]() ,
,
在△HGM中, ∠AGD+∠BHG +∠GMH=![]() ,
,
∴∠GMH=![]() ,
,
则DG⊥BE;
②根据①可知旋转过程中,DG=BE且DG⊥BE;
当BE取得最大值,即点A,B,E在同一条直线上时,四边形BGED面积有最大值.
此时:DG=BE![]()
四边形BGED面积![]()
(2)连接BE,DG,
根据中位线的性质可得![]()
![]()
![]() ,
,![]() ,
,
![]()
![]()
![]()
四边形MNPQ是正方形,边长的最大值为![]()
四边形MNPQ面积的最大值是:![]()
故答案为:正方形,3+2![]() .
.