题目内容
【题目】已知:点A在射线CE上,∠C=∠D.
⑴如图1,若AD∥BC,求证:BD∥AC;
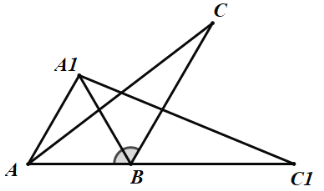
⑵如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
⑶如图3,在⑵的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

【答案】(1)见解析;(2)∠DAE+2∠C=90 ;(3)99°
【解析】
(1)根据AC∥BD,可得∠DAE=∠D,再根据∠C=∠D,即可得到∠DAE=∠C,进而判定AD∥BC;
(2)根据∠CGB是△ADG是外角,即可得到∠CGB=∠D+∠DAE,再根据△BCG中,∠CGB+∠C=90°,即可得到∠D+∠DAE+∠C=90°,进而得出2∠C+∠DAE=90°;
(3)设∠DAE=α,则∠DFE=8α,∠AFD=180°-8α,根据DF∥BC,即可得到∠C=∠AFD=180°-8α,再根据2∠C+∠DAE=90°,即可得到2(180°-8α)+α=90°,求得α的值,即可运用三角形内角和定理得到∠BAD的度数.
解:(1)∵AC∥BD,
∴∠DAE=∠D,
又∵∠C=∠D,
∴∠DAE=∠C,
∴AD∥BC;
(2)∠EAD+2∠C=90°.
证明:设CE与BD交点为G,
∵∠CGB是△ADG是外角,
∴∠CGB=∠D+∠DAE,
∵BD⊥BC,
∴∠CBD=90°,
∴△BCG中,∠CGB+∠C=90°,
∴∠D+∠DAE+∠C=90°,
又∵∠D=∠C,
∴2∠C+∠DAE=90°;
(3)设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=![]() ∠CBD=45°,
∠CBD=45°,
∴△ABD中,∠BAD=180°﹣45°﹣36°=99°.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案