题目内容
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE= ![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.

【答案】证明:过点C分别作OA,OB的垂线,垂足分别为P,Q.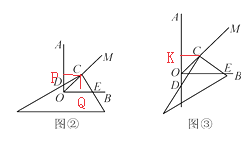
有△CPD≌△CQE,
∴DP=EQ,
∵OP=OD+DP,OQ=OE-EQ,
又∵OP+OQ= ![]() OC,
OC,
即OD+DP+OE-EQ= ![]() OC,
OC,
∴OD+OE= ![]() OC.
OC.
图③不成立,
有数量关系:OE-OD= ![]() OC
OC
过点C分别作CK⊥OA, CH⊥OB, ∵OC为∠AOB的角平分线,且CK⊥OA,CH⊥OB, ∴CK=CH,∠CKD=∠CHE=90°, 又∵∠KCD与∠HCE都为旋转角, ∴∠KCD=∠HCE, ∴△CKD≌△CHE, ∴DK=EH, ∴OE-OD=OH+EH-OD=OH+DK-OD=OH+OK, 由(1)知:OH+OK= ![]() OC, ∴OD,OE,OC满足OE-OD=
OC, ∴OD,OE,OC满足OE-OD= ![]() OC.
OC.
【解析】模仿第1种特例,过点C作垂线,构造出全等的三角形,即△CPD≌△CQE,由对应边相等可得出另两个类似的结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







