题目内容
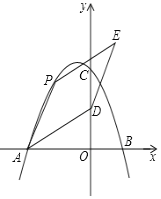
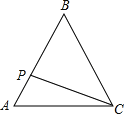
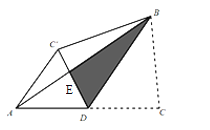
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接CC′,交BD于点M,过点D作DH⊥BC于点H,由翻折知,△BDC≌△BDC’,BD垂直平分CC,证△ADC为等边三角形,利用解直角三角形求出DM=1,CM=![]() =
=![]() ,BM=2,在Rt△BMC'中,利用勾股定理求出BC′的长,在△BDC中利用面积法求出DH的长.
,BM=2,在Rt△BMC'中,利用勾股定理求出BC′的长,在△BDC中利用面积法求出DH的长.
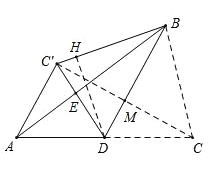
解:如图,连接CC′,交BD于点M,过点D作DH⊥BC′于点H,
∵AD=AC'=2,D是AC边上的中点,
∴DC=AD=2,
由翻折知,△BDC≌△BDC′,BD垂直平分CC′,
∴DC=DC′=2,BC=BC′,CM=C′M,
∴AD=AC'=DC′=2,
∴△ADC′为等边三角形,
∴∠ADC=∠AC′D=∠C′AC=60°,
∵DC=DC′,
∴∠DCC′=∠DC′C=![]() ×60°=30°,
×60°=30°,
在Rt△CDM中,∠DC′C=30°,DC′=2,
∴DM=1,C′M=![]() DM=
DM=![]() ,
,
·.BM=BD-DM=3-1=2,
在Rt△BMC中,BC′=![]()
![]()
![]()
∴.BM=BD-DM=3-1=2,
在Rt△C'DM中,![]()
![]()
∴![]()
∴![]()
故选B.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目