Question

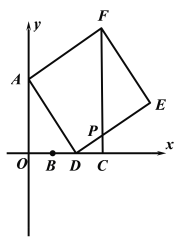
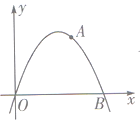
【题目】如图，抛物线交轴于、两点，为抛物线上一点，且横纵坐标相等(原点除外)，为抛物线上一动点，过作轴的垂线，垂足为，并与直线交于点.

(1)求、两点的坐标.

(2)当点在线段上方时，过作轴的平行线与直线相交于点，求周长的最大值及此时点的坐标.

Answer 1

【答案】(1)点坐标为，点的坐标为；(2)周长的最大值为，点坐标为.

【解析】

（1）利用待定系数法即可解决问题；

（2）设点的坐标为，则,Q点的坐标为（n，0），轴,得出是等腰直角三角形，进而得出当取最大值时，周长最大， PC即可用含a的代数式表示出来，利用二次函数的性质即可解决最值问题

解：(1)令，则，

解得，，

∴点坐标为，

设点坐标为，把代入得，

，

解得，(舍去)，

∴点的坐标为；

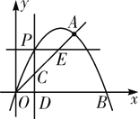
(2)如图，设点的坐标为，

∵点坐标为，

∴，

∴，

∴.

∵轴，

∴是等腰直角三角形，

∴当取最大值时，周长最大.

∵与线段相交，

∴.

由可知，抛物线的对称轴为直线，在对称轴左侧随的增大而增大.

∴当时，最大，的最大值为

∴，，

∴的周长为.

∴周长的最大值为，

把代入的坐标，得

∴点坐标为.