��Ŀ����
����Ŀ�����꼶ѧ��С�Ϻ�С���������ѧʵ�顶�����ϵ���ѧ��֮��������һ��ģ�����棬��ͼ��ʾ��O Ϊģ������Բ�ģ�M��O��N ��һ��ֱ���ϣ�ָ�� OA��OB �ֱ�� OM��ON �����Ƶ� O ת����OA �˶��ٶ�Ϊÿ�� 15�㣬OB �˶��ٶ�Ϊÿ�� 5�㣬��һ��ָ������ʼλ���غ�ʱ���˶�ֹͣ����ת����ʱ��Ϊ t �룬�������Ž������������������⣺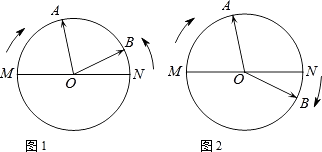
��1����OA˳ʱ��ת����OB��ʱ��ת����t=��ʱ��OA��OB��һ���غϣ�
��2��������ͬʱ˳ʱ��ת��
�ٵ� t=3 ��ʱ����AOB=�㣻
���𰸡�
��1��9
��2��150�ڵ� t Ϊ��ֵʱ,OA �� OB ��һ���غϣ��⣺��t����һ���غϣ�15t��5t=180,t=18����t=18��ʱ,��һ���غϢ۵� t Ϊ��ֵʱ,��AOB=30�㣿�⣺��t����AOB=30��,������15t��5t=180-30��15t��5t=180+30,��t=15��21����t=15��21��ʱ,��AOB=30��
����������1����t����һ���غϣ���15+5��t=180,t=9.��2������ͼ2�У�t=3ʱ����AOM=45����AON=135����BON=15�����AOB=��AON+��BON=150��
��1����������д����ȵĹ�ϵ������OA˳ʱ��ת����OB��ʱ��ת�������������⣬����180�ȣ��õ��������t��ֵ����2��������ͬʱ˳ʱ��ת�������������⣬��t=3ʱ���õ���AOB=��AON+��BON��ֵ����OA��OB��һ���غ�ʱ���õ�����15t��5t=180�����t��ֵ������AOB=30��ʱ���õ�����15t��5t=180-30��15t��5t=180+30�����t��ֵ.

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�����Ŀ��ij��ѧ���С��ж���������־�ɲš��ݽ����������ݳ����ɼ����ߣ����꼶�ֱ�ѡ��10��ͬѧ�μӾ�������Щѡ�ֵľ����ɼ���ͼ��ʾ��
����ͼ���±��ṩ����Ϣ������������⣺
��1��������±ߵı�����д������
�ɼ�ͳ�� | ���� | ƽ���� | ���� |
���꼶 | 85.7 | 39.61 | |
���꼶 | 85.7 | 27.81 |
��2������ƽ�����뷽�����Ϊ���꼶������ɼ�����Щ��
��3��������ÿ���꼶�ľ���ѡ���зֱ�ѡ��3�˲μ��ܾ���������Ϊ�ĸ��꼶��ʵ����ǿһЩ����˵������.