Question

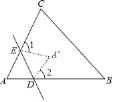
【题目】如图，AB∥CD，∠A＝90°，E是AD边的中点，CE平分∠BCD．

（1）求证：BE平分∠ABC；

（2）若AB＝2，CD＝1，求BC的长．

Answer 1

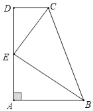
【答案】(1)见解析;(2)3.

【解析】

（1）由角平分线的性质可得ED＝EM，由角平分线的判定可证BE平分∠ABC；

（2）由全等三角形的性质可得DC＝CM＝1，AB＝BM＝2，即可求BC的长．

证明：（1）如图，作EM⊥BC于点M，

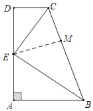
∵EC平分∠DCB，ED⊥CD，EM⊥BC

∴ED＝EM

又∵DE＝AE，且EA⊥AB，EM⊥BC

∴BE平分∠ABC

（2）∵DE＝EM，CE＝CE

∴Rt△DCE≌Rt△MCE（HL）

∴DC＝CM＝1

同理可得AB＝BM＝2

∴BC＝CM+BM＝CD+AB＝3