题目内容
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知:
如图①⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1="1;"
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.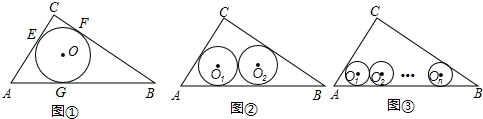
(Ⅰ)探究新知:
如图①⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1="1;"
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.

(Ⅰ)探究新知(1)证明见解析(2)1/2(Ⅱ)结论应用(1)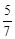 (2)
(2)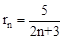
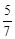 (2)
(2)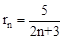
解:(Ⅰ)(1)证明:在图①中,连接OE,OF。
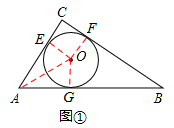
∵点E、F、G是⊙O的切点
∴四边形CEOF是正方形, CE=CF=r1。
又∵AC=3,BC=4,AB=5,
∴AG=AE=3-r1,BG=BF=4-r1,AG+BG=5。
∴(3-r1)+(4-r1)=5,解得r1=1。
(2)连接OG,OA在Rt△AOG中,∵OG=r1=1, AG= 3-r1=2,
∴tan∠OAG=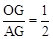 。
。
(Ⅱ)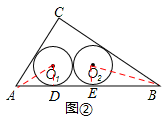
(1)连接O1A、O2B,作O1D⊥AB交于点D、O2E⊥AB交于点E。
则 AO1、BO2分别平分∠CAB、∠ABC。
由(Ⅰ)tan∠OAG=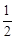 ,知tan∠O1AD=
,知tan∠O1AD=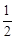 ,
,
同理可得:tan∠O2BE=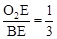 。
。
∴AD=2r2,DE=2r2,BE=3r2。
∵AD+DE+BE=5,∴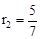 。
。
(2)如图③,
连接O1A、OnB,作O1D⊥AB交于点D、O2E⊥AB交于点E、…、OnF⊥AB交于点F。则AO1、BO2分别平分∠CAB、∠ABC。
tan∠O1AD=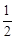 ,tan∠OnBF=
,tan∠OnBF=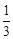 ,
,
∴AD=2rn,DE=2rn,…,FB=3rn。
又∵AD+DE+…+FB=5,2rn+2rn+…+3rn=5,即(2n+3) rn=5,
∴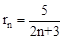 。
。
(Ⅰ)(1)由切线的性质可得四边形CEOF是正方形,从而由AG=AE=3-r1,BG=BF=4-r1,AG+BG=5可证得内切圆的半径r1=1。
(2)根据锐角三角函数定义直接求得。
(Ⅱ)(1)由(Ⅰ)的结论得tan∠O1AD=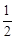 ,同理可推得tan∠O2BE=
,同理可推得tan∠O2BE=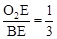 ,从而由AD=2r2,DE=2r2,BE=3r2和AD+DE+BE=5可求得r2的值。
,从而由AD=2r2,DE=2r2,BE=3r2和AD+DE+BE=5可求得r2的值。
(2)由(Ⅱ)(1)有tan∠O1AD=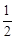 ,tan∠OnBF=
,tan∠OnBF=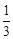 ,从而由AD=2rn,DE=2rn,…,FB=3rn和AD+DE+…+FB=5,2rn+2rn+…+3rn=5可求得rn的值。
,从而由AD=2rn,DE=2rn,…,FB=3rn和AD+DE+…+FB=5,2rn+2rn+…+3rn=5可求得rn的值。

∵点E、F、G是⊙O的切点
∴四边形CEOF是正方形, CE=CF=r1。
又∵AC=3,BC=4,AB=5,
∴AG=AE=3-r1,BG=BF=4-r1,AG+BG=5。
∴(3-r1)+(4-r1)=5,解得r1=1。
(2)连接OG,OA在Rt△AOG中,∵OG=r1=1, AG= 3-r1=2,
∴tan∠OAG=
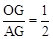 。
。(Ⅱ)

(1)连接O1A、O2B,作O1D⊥AB交于点D、O2E⊥AB交于点E。
则 AO1、BO2分别平分∠CAB、∠ABC。
由(Ⅰ)tan∠OAG=
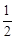 ,知tan∠O1AD=
,知tan∠O1AD=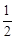 ,
,同理可得:tan∠O2BE=
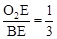 。
。 ∴AD=2r2,DE=2r2,BE=3r2。
∵AD+DE+BE=5,∴
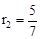 。
。(2)如图③,

连接O1A、OnB,作O1D⊥AB交于点D、O2E⊥AB交于点E、…、OnF⊥AB交于点F。则AO1、BO2分别平分∠CAB、∠ABC。
tan∠O1AD=
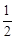 ,tan∠OnBF=
,tan∠OnBF=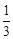 ,
,∴AD=2rn,DE=2rn,…,FB=3rn。
又∵AD+DE+…+FB=5,2rn+2rn+…+3rn=5,即(2n+3) rn=5,
∴
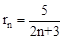 。
。(Ⅰ)(1)由切线的性质可得四边形CEOF是正方形,从而由AG=AE=3-r1,BG=BF=4-r1,AG+BG=5可证得内切圆的半径r1=1。
(2)根据锐角三角函数定义直接求得。
(Ⅱ)(1)由(Ⅰ)的结论得tan∠O1AD=
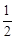 ,同理可推得tan∠O2BE=
,同理可推得tan∠O2BE=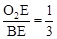 ,从而由AD=2r2,DE=2r2,BE=3r2和AD+DE+BE=5可求得r2的值。
,从而由AD=2r2,DE=2r2,BE=3r2和AD+DE+BE=5可求得r2的值。(2)由(Ⅱ)(1)有tan∠O1AD=
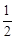 ,tan∠OnBF=
,tan∠OnBF=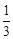 ,从而由AD=2rn,DE=2rn,…,FB=3rn和AD+DE+…+FB=5,2rn+2rn+…+3rn=5可求得rn的值。
,从而由AD=2rn,DE=2rn,…,FB=3rn和AD+DE+…+FB=5,2rn+2rn+…+3rn=5可求得rn的值。
练习册系列答案
相关题目
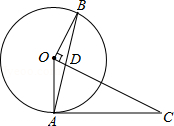
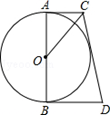
 cm2.
cm2.
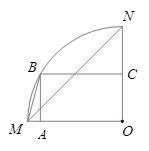
 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦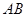 是小圆的切线.若大圆半径为
是小圆的切线.若大圆半径为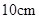 ,小圆半径为
,小圆半径为 ,则弦
,则弦