题目内容
【题目】如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.
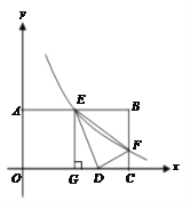
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.
【答案】(1)点F的坐标为(4,1);(2)证明见解析,k=3.
【解析】
试题分析:(1)根据点E是AB中点,可求出点E的坐标,将点E的坐标代入反比例函数解析式可求出k的值,再由点F的横坐标为4,可求出点F的纵坐标,继而得出答案;
(2)证明∠GED=∠CDF,然后利用两角法可判断△EGD∽△DCF,设点E坐标为(![]() ,2),点F坐标为(4,
,2),点F坐标为(4,![]() ),即可得CF=
),即可得CF=![]() ,BF=DF=2﹣
,BF=DF=2﹣![]() ,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值.
,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值.
试题解析:(1)∵点E是AB的中点,OA=2,AB=4,
∴点E的坐标为(2,2),
将点E的坐标代入y=![]() ,可得k=4,
,可得k=4,
即反比例函数解析式为:y=![]() ,
,
∵点F的横坐标为4,
∴点F的纵坐标=![]() =1,
=1,
故点F的坐标为(4,1);
(2)由折叠的性质可得:BE=DE,BF=DF,∠B=∠EDF=90°,
∵∠CDF+∠EDG=90°,∠GED+∠EDG=90°,
∴∠CDF=∠GED,
又∵∠EGD=∠DCF=90°,
∴△EGD∽△DCF,
结合图形可设点E坐标为(![]() ,2),点F坐标为(4,
,2),点F坐标为(4,![]() ),
),
则CF=![]() ,BF=DF=2﹣
,BF=DF=2﹣![]() ,ED=BE=AB﹣AE=4﹣
,ED=BE=AB﹣AE=4﹣![]() ,
,
在Rt△CDF中,CD=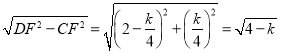 ,
,
∵![]() ,即
,即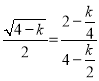 ,
,
∴![]() =1,
=1,
解得:k=3.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周) | 小明抽样人数 | 小华抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
【题目】2019年,在嵊州市道路提升工程中,甲、乙两个工程队分别承担道路绿化和道路拓宽工程。已知道路绿化和道路拓宽工程的总里程数是8.6千米,其中道路绿化里程数是道路拓宽里程数的2倍少1千米。
(1)求道路绿化和道路拓宽里程数分别是多少千米;
(2)甲、乙两个工程队同时开始施工,甲工程队比乙工程队平均每天多施工10米。由于工期需要,甲工程队在完成所承担的![]() 施工任务后,通过技术改进使工作效率比原来提高
施工任务后,通过技术改进使工作效率比原来提高![]() ,设乙工程队平均每天施工
,设乙工程队平均每天施工![]() 米,请回答下列问题:
米,请回答下列问题:
①根据题意,填写下表:
乙工程队 | 甲工程队 | ||
技术改进前 | 技术改进后 | ||
施工天数(天)(用含 | |||
②若甲、乙两队同时完成施工任务,求乙工程队平均每天施工的米数![]() 和施工的天数。
和施工的天数。