题目内容
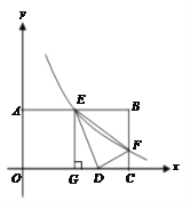
【题目】在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S矩形ABCD=3S△PAB,则PA+PB的最小值为_____.
【答案】4![]()
【解析】
首先由S矩形ABCD=3S△PAB,得出动点P在与AB平行且与AB的距离是2的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
设△ABP中AB边上的高是h.
∵S矩形ABCD=3S△PAB,
∴![]() ABh=
ABh=![]() ABAD,
ABAD,
∴h=![]() AD=2,
AD=2,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
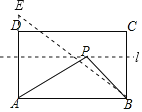
在Rt△ABE中,∵AB=4,AE=2+2=4,
∴BE=![]() ,
,
即PA+PB的最小值为4![]() .
.
故答案为:4![]() .
.

【题目】我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确数字x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.

【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.

调查结果统计表
组别 | 分组 | 人数 |
A |
| 4 |
B |
| 16 |
C |
| a |
D |
| b |
E |
| 2 |
请根据以上图表,解答下列问题:
![]() 填空:这次被调查的同学共有______ 人,
填空:这次被调查的同学共有______ 人, ![]() ______ ,
______ , ![]() ______ ;
______ ;
![]() 求扇形统计图中扇形C的圆心角度数;
求扇形统计图中扇形C的圆心角度数;
![]() 该校共有学生1000人,请估计每月零花钱的数额x在
该校共有学生1000人,请估计每月零花钱的数额x在![]() 范围的人数.
范围的人数.