题目内容
【题目】如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果Q、P分别从A、B两点出发,那么几秒后,△PBQ的面积等于8cm2?
(2)在(1)中,△PBQ的面积能否等于10cm2?试说明理由.
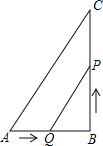
【答案】(1)2秒或4秒后,△PBQ的面积等于8cm2(2)△PBQ的面积不能等于10cm2
【解析】
(1)分别表示出线段PB和线段BQ的长,然后根据面积为8列出方程求得时间即可;
(2)根据面积为10列出方程,判定方程是否有解即可.
(1)设t秒后,△PBQ的面积等于8cm2,根据题意得:
![]() 2t(6﹣t)=8
2t(6﹣t)=8
解得:t=2或4.
答:2秒或4秒后,△PBQ的面积等于8cm2.
(2)由题意得:![]() 2t(6﹣t)=10
2t(6﹣t)=10
整理得:t2﹣6t+10=0
∵b2﹣4ac=36﹣40=﹣4<0,此方程无解,所以△PBQ的面积不能等于10cm2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
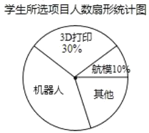
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m= ,n= ;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 °;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.