题目内容
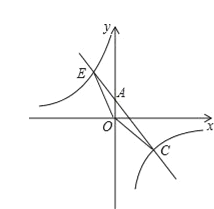
【题目】如图，反比例函数y=
的图象与一次函数y=ax﹢b的图象交于C（4，﹣3），E（﹣3，4）两点．且一次函数图象交y轴于点A．
（1）求反比例函数与一次函数的解析式；
（2）求△COE的面积；
（3）点M在x轴上移动，是否存在点M使△OCM为等腰三角形？若存在，请你直接写出M点的坐标；若不存在，请说明理由．
【答案】（1）一次函数的解析式为y=﹣x+1．
（2）S△COE=S△AOE+S△AOC=
×1×3+
×1×4=3.5．
（3）点M坐标为M1（8，0）或M2（5，0）或M3（﹣5，0）或M4（
，0）．
【解析】
试题分析：（1）点C（4，﹣3）坐标代入反比例函数y=
即可求出k，C（4，﹣3），E（﹣3，4）两点坐标代入y=ax+b解方程组即可求出a、b．由此即可解决问题．
（2）先求出点A坐标，根据S△COE=S△AOE+S△AOC计算即可．
（3）分三种情形①当CM=OC时，可得M1（8，0）．②当OC=OM时，可得M2（5，0），M3（﹣5，0）．②当MC=MO时，设M4（x，0），则有x2=（x﹣4）2+32，解方程即可．
试题解析：（1）∵反比例函数y=的图象经过点C（4，﹣3），
∴﹣3=
，∴k=﹣12，∴反比例函数解析式为y=﹣
，
∵y=ax+b的图象经过C（4，﹣3），E（﹣3，4）两点，
∴
，解得
，∴一次函数的解析式为y=﹣x+1．
（2）∵一次函数的解析式为y=﹣x+1与y轴交于点A（0，1），∴S△COE=S△AOE+S△AOC=×1×3+×1×4=3.5．
（3）如图，∵C（4，﹣3），∴OC=
=5，
①当CM=OC时，可得M1（8，0）．②当OC=OM时，可得M2（5，0），M3（﹣5，0）．
②当MC=MO时，设M4（x，0），则有x2=（x﹣4）2+32，解得x=，∴M4（
，0）．
综上所述，点M坐标为M1（8，0）或M2（5，0）或M3（﹣5，0）或M4（，0）．
