Question

【题目】在初中阶段的函数学习中，我们经历了“确定函数的解析式利用函数图象研究其性质﹣运用函数解决问题”的学习过程．在画函数图象时，我们可以通过描点或平移或翻折等方法画出函数图象、下面我们対函数y＝|﹣1|展开探索，请补充以下探索过程：

（1）列表

x

…

﹣1

﹣

﹣

﹣

0

…

2

3

…

y

…

2

3

a

…

3

1

0

b

…

直接写出函数自变量x的取值范围，及a＝　 　，b＝　 　；

（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象，并写出这个函数的一条性质：　 　．

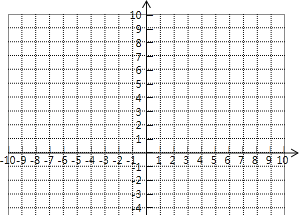
（3）若方程|﹣1|＝m有且只有一个解，直接写出m的值：　 　．

Answer 1

【答案】（1）5，；（2）画出这个函数的图象见解析；1＜x＜2时，y随x值的增大而减小;（3）1．

【解析】

（1）根据分母不能为0即可写出自变量的取值范围；利用函数解析式分别求出对应的函数值即可；利用描点法画出图象即可；

（2）利用描点法画出图象，观察图象可知：①1＜x＜2时，y随x值的增大而减小；

（3）利用图象即可解决问题．

（1）∵x﹣1≠0，

∴x≠1，

∴函数y＝|﹣1|的自变量x的取值范围是x≠1，

把x＝和分别代入函数关系式求得a＝5，b＝

故答案为5，．

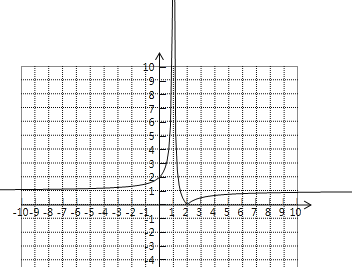
（2）函数y＝|﹣1|的图象如图所示，

由图可知，1＜x＜2时，y随x值的增大而减小；

（3）由图象可知，m＝1时，方程|﹣1|＝m有且只有一个解，

解为x＝1.5，

故答案为1．